Student Library

The Limit Laws

9 min read

Objectives

  • Define the algebraic limit laws
  • Use the limit laws to evaluate the limit of a polynomial function.
  • Use the limit laws to evaluate the limit of a rational function.
  • Use the limit laws to evaluate the limit of a radical function.

Algebraic Limit Laws

  • Before, we have been using tables and graphs to approximate the true value of a limit of a function.
    • However, some of these functions can be broken down into its individual parts, which we can then use to compute the limit.
    • But before we do that, we first introduce the two most basic limit laws: the constant and identity limit laws.

Definition
Basic Limit Laws

Let be any real number constant.

  • The first rule makes sense since if the function is a constant, then regardless of the value we are approaching, the limit is equal to the constant itself.
  • The second rule also makes sense.
    • As we approach the function at any point , the value of the limit eventually approach the value we want to approach.

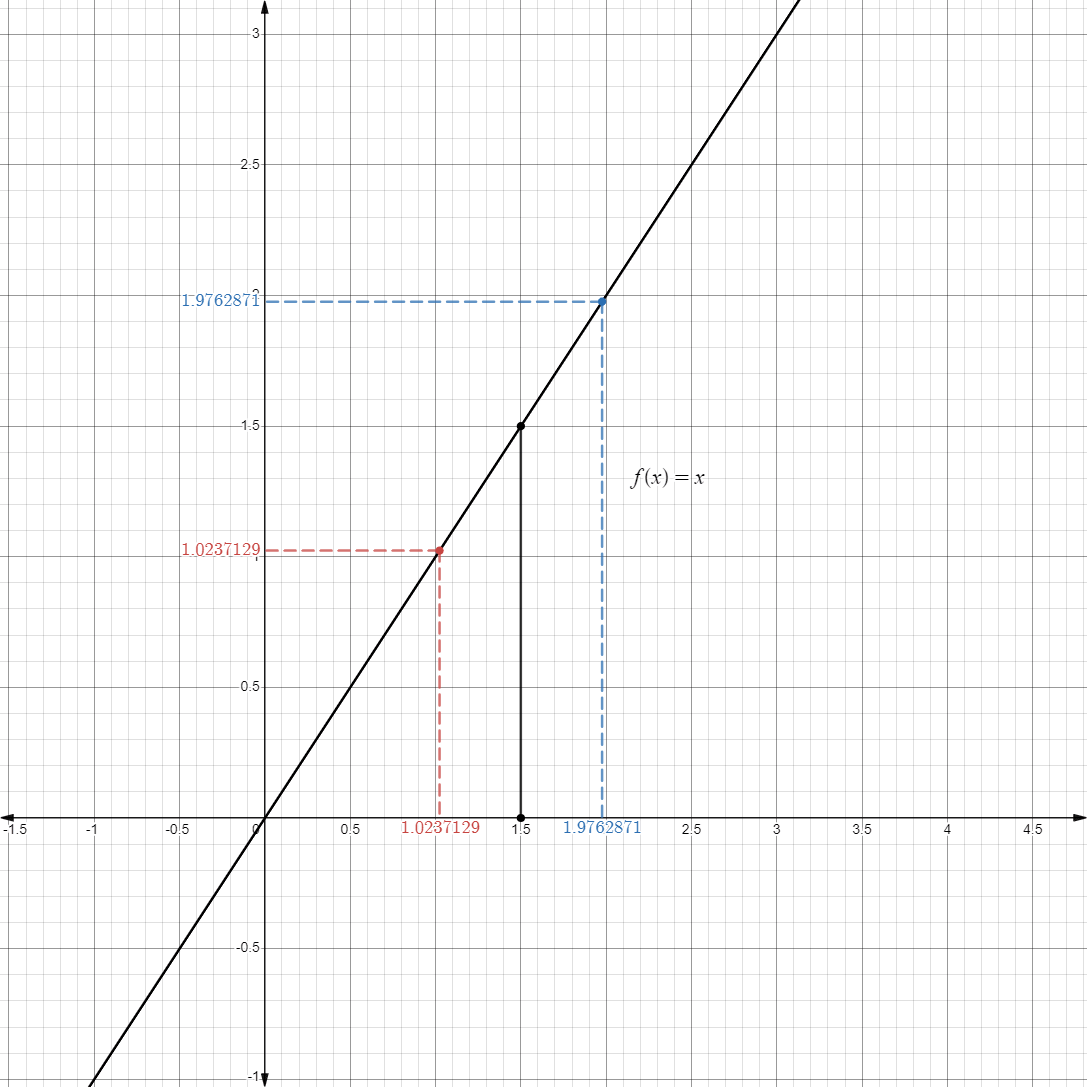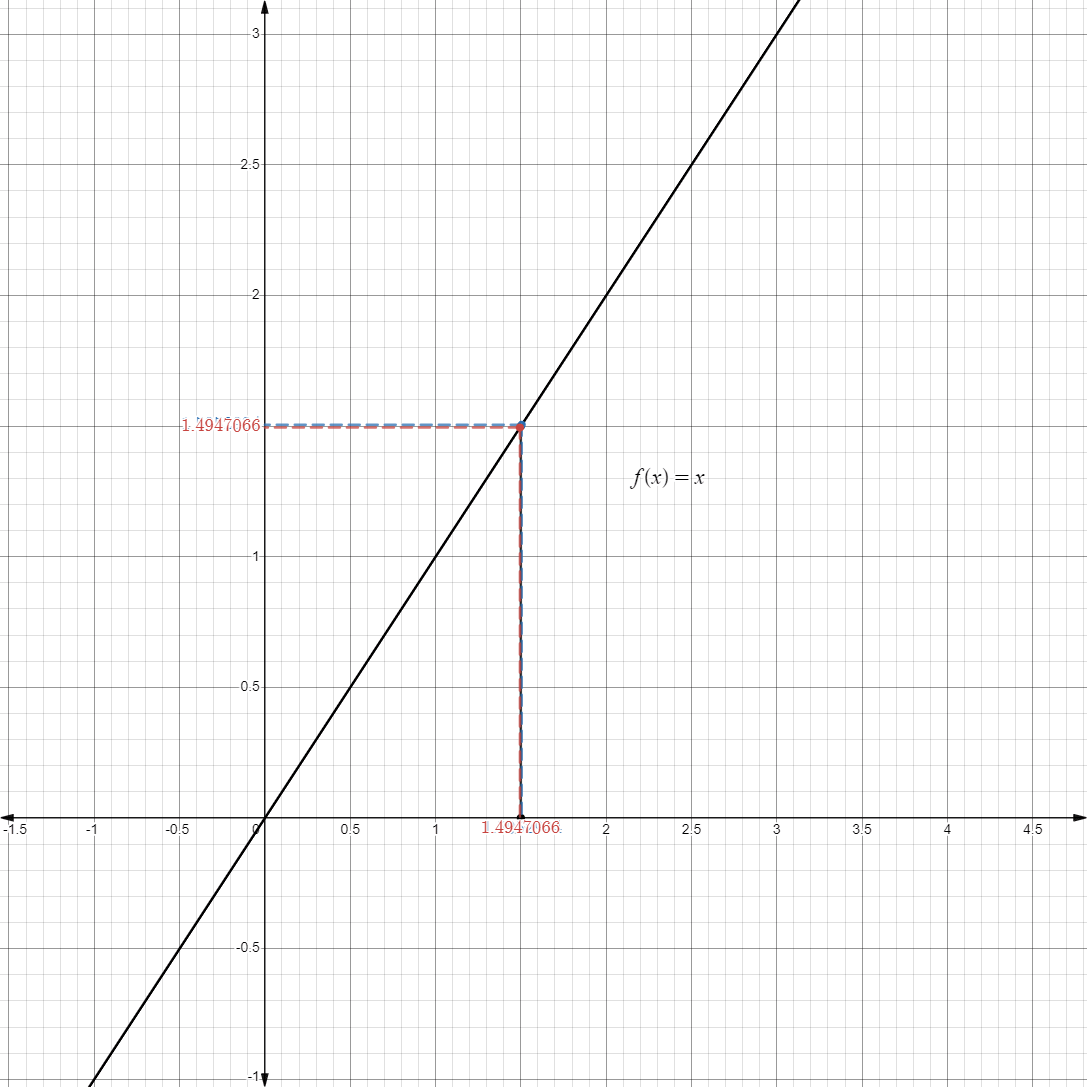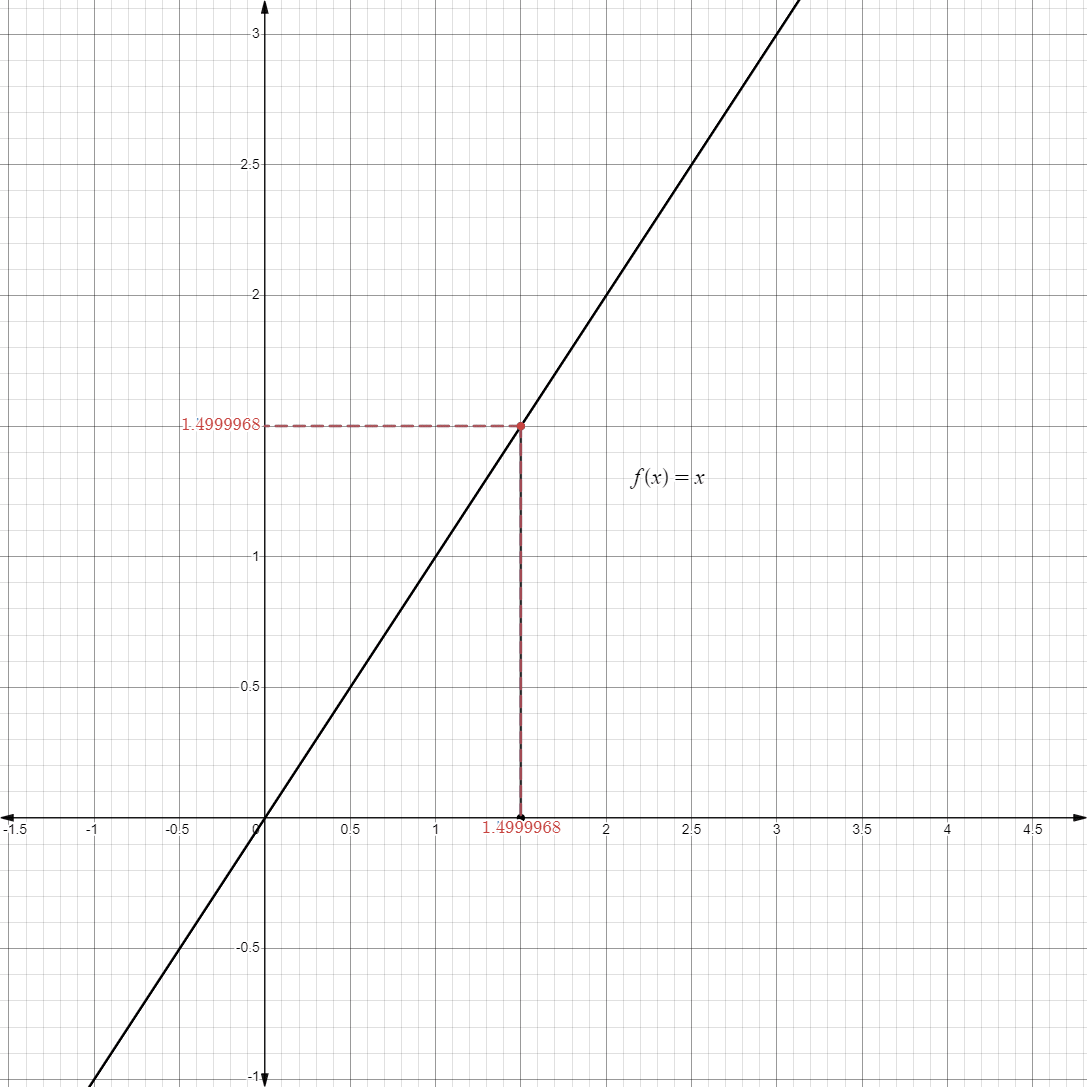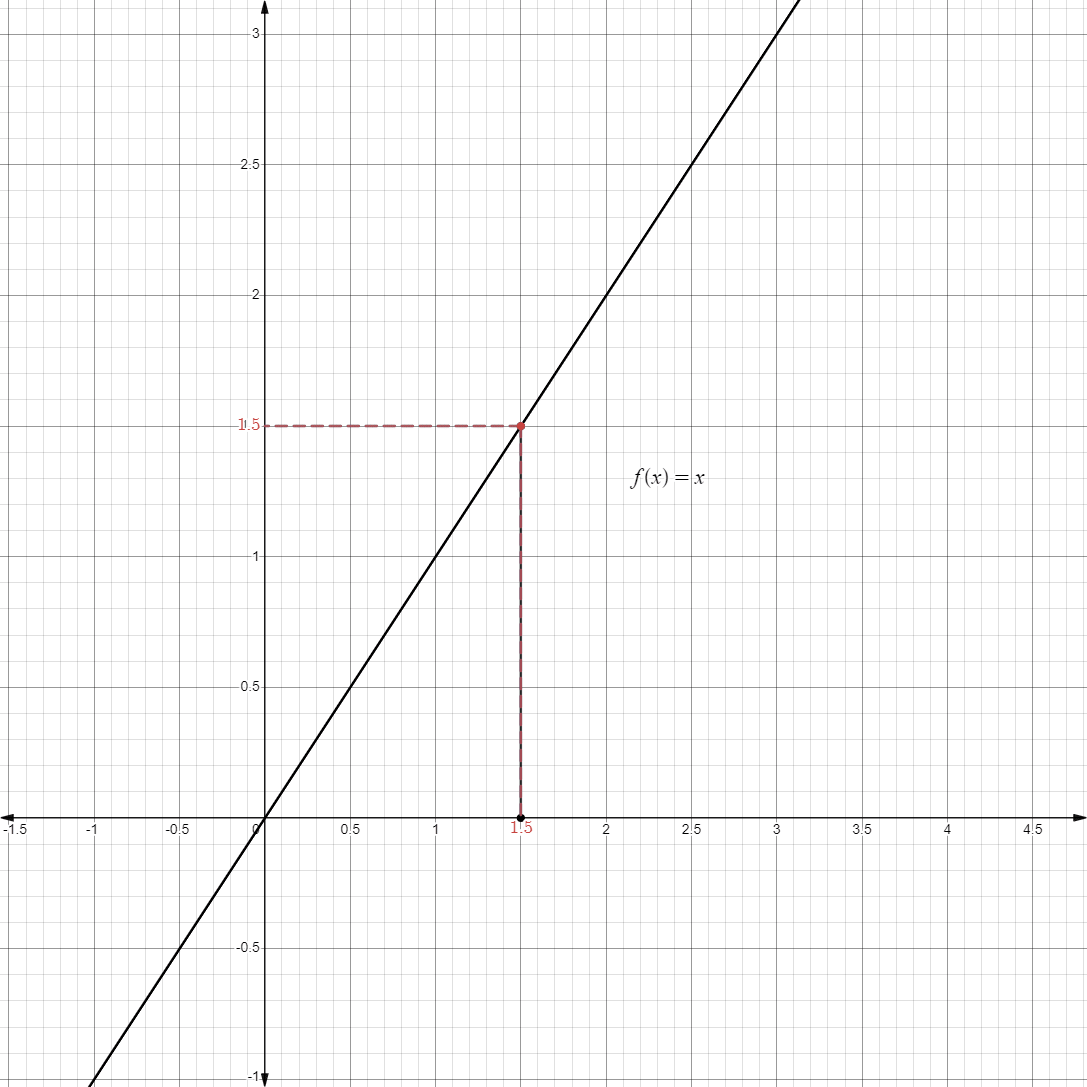
  • Now that we have established this, we now introduce the algebraic limit laws

Definition
Algebraic Limit Laws

Let and be functions and be constants. If there exist finite, real numbers and , where:

then these following rules should apply.

  • To practice working with these rules, let us work on the following limit below:
  • First, we can use the difference rule to express the statement into two separate limits.
  • The limit can be broken down further using the constant multiple rule.
  • We have now broken our limit enough that we can now use the basic limit laws to evaluate them.
  • Therefore:

Evaluating Limits of Polynomial Functions

  • When we evaluate the limit of a polynomial function, we use the sum, difference and power rules to simplify the limit even further.
    • The goal is to break the limit of a polynomial function into multiple limits that can be evaluated using the basic limit laws.

Worked Example 1
Evaluating the Limit of a Quadratic Function

Evaluate .

Worked Example 2
Evaluating the Limit of a Cubic Function

Evaluate .

Evaluating Limits of Rational Functions

  • Similar to how polynomial functions can be broken into smaller limits the same goes for rational functions.
    • We first use the quotient rule break the limit of a rational function into the limit of the numerator over the limit of the denominator.
  • Then, we use the sum, difference, constant multiple, and power limit laws to break the numerator and denominator into simpler limits.

Worked Example 3
Evaluating the Limit of a Rational Function

Evaluate .

  • One important caveat here is that the limit of the denominator must not equal to .
    • This could indicate a division by zero.
    • Therefore, if that is the case, then the limit of the rational function does not exist.

Worked Example 4
Evaluating the Limit of a Rational Function that Doesn't Exist

Evaluate .

Evaluating Limits of Radical Functions

  • Suppose that we have the limit below.
  • By knowing that is the same as , we can then use the power rule.
  • Therefore, as an extension to the Power Law, we now introduce the Root Law.

Definition
Root Law of Limits

Let and be a constant where and . Given that where is some finite, real number, then these rules apply.

  • If is odd, then:
  • If is even, then:

If is even and the limit of is less than , then the limit does not exist.

Graph View