Limit of a Function

Objectives

Define the concept of a limit

Use a table of values to evaluate simple limits.

Use a graph to evaluate simple limits.

Evaluate a limit by substitution.

What is a Limit?

The limit of a function at a point is the value of a function as it approaches on that point.
For example, take a look at the function .
- What does it mean to take the limit of as it approaches to ?
- One way we can do this is by taking values that get closer and closer to .

We can see that as we take values closer to , we slowly approach the value .
Symbolically, we can express it as:

Definition
Informal Definition of a Limit

A limit of a function at any point is a real valued number where as approaches , the value of approaches .

Mathematically, this statement can be expressed as:

Using Tables to Evaluate Limits

Just like before, we can use a table to evaluate limits.
For instance, let us find the limit of the function:

Like from before, we can set-up a table of values approaching from .

We can also set-up a table of values approaching from .

Therefore:

Using Graphs to Evaluate Limits

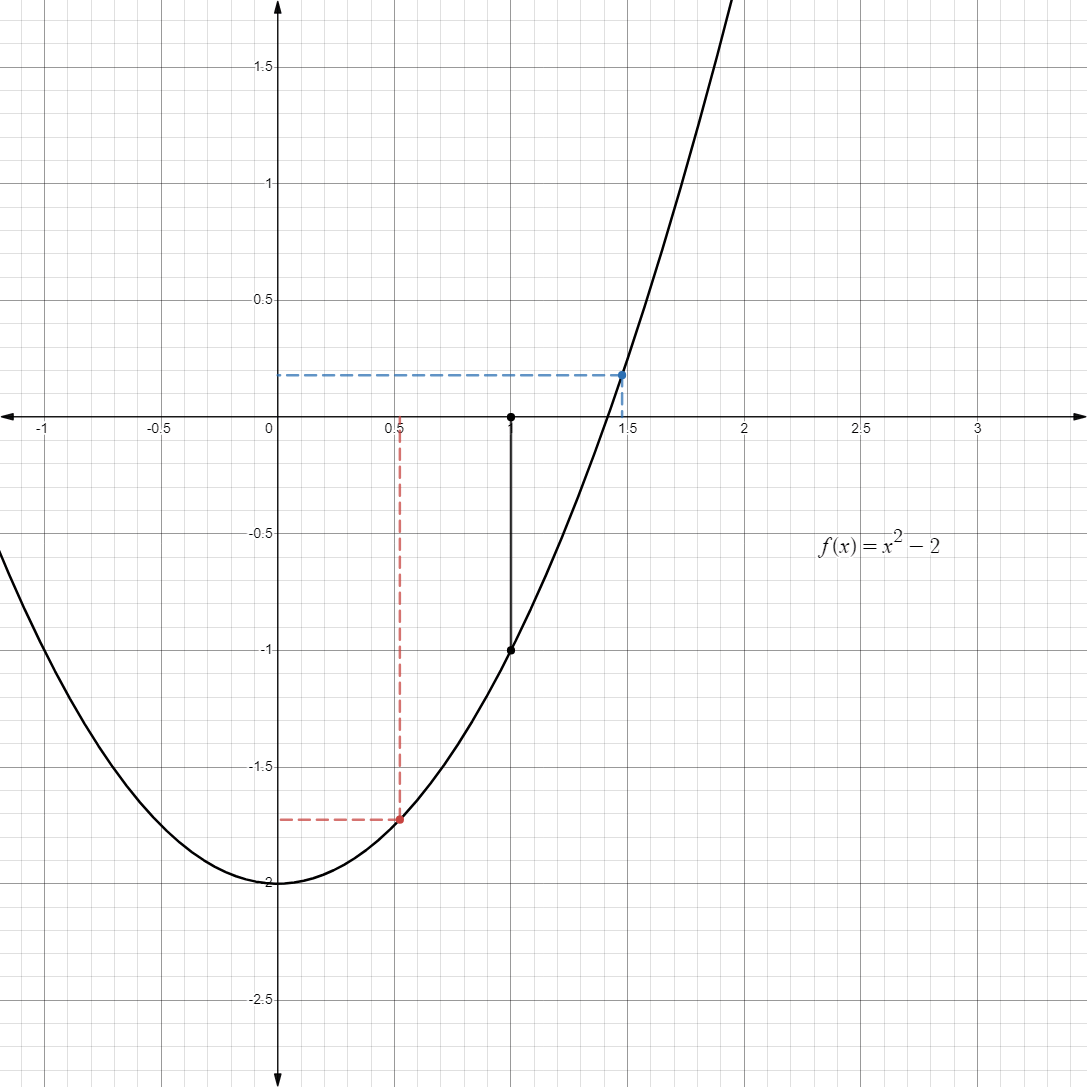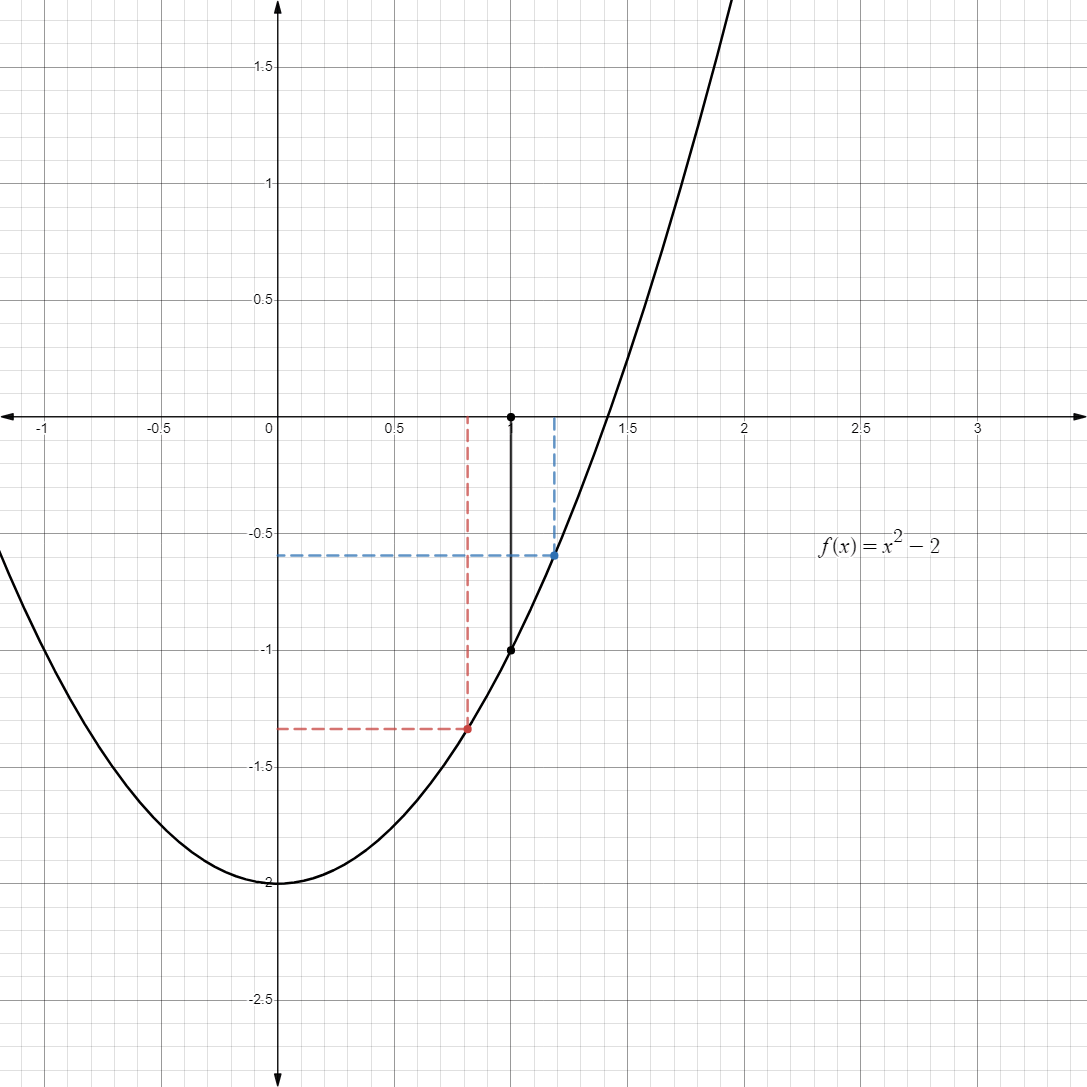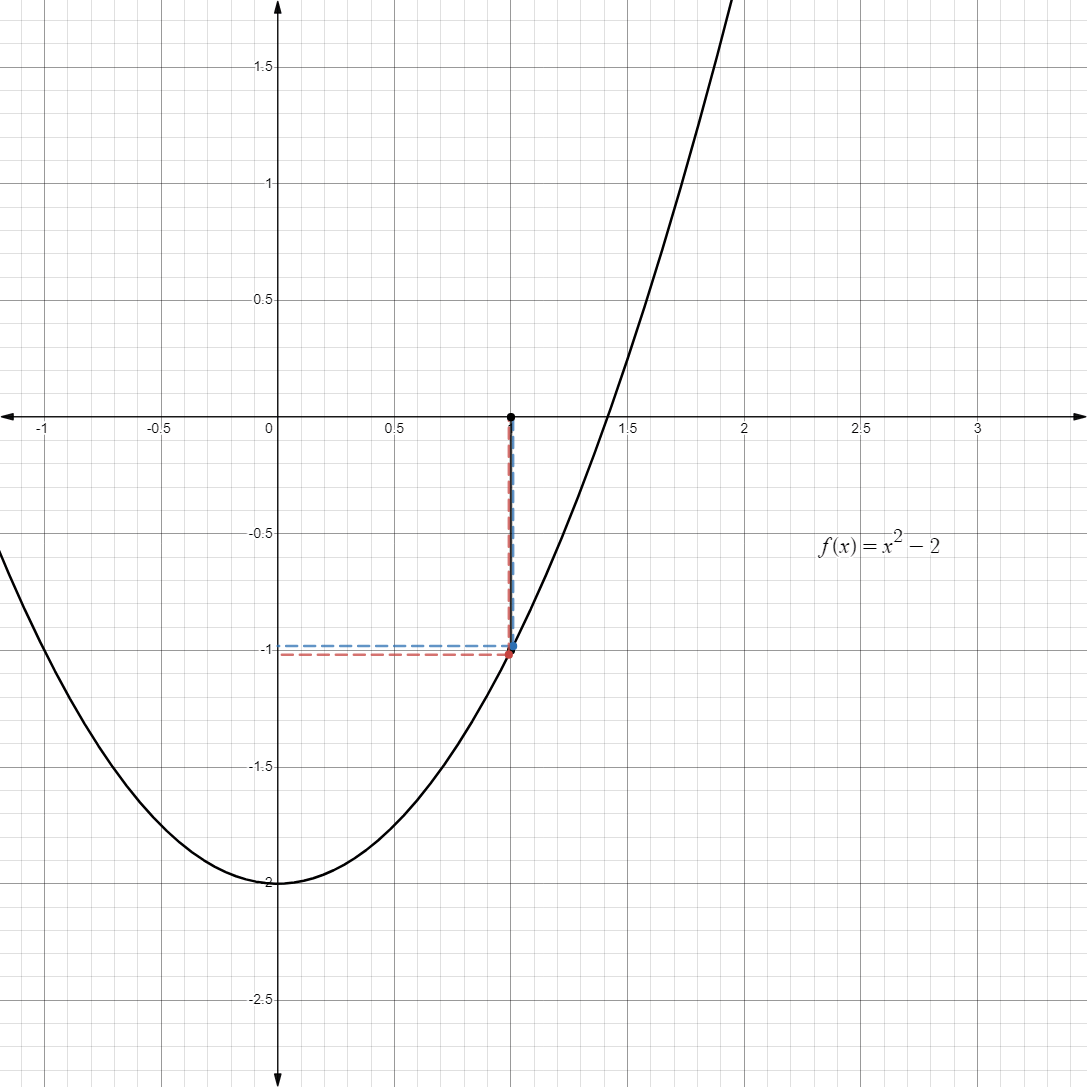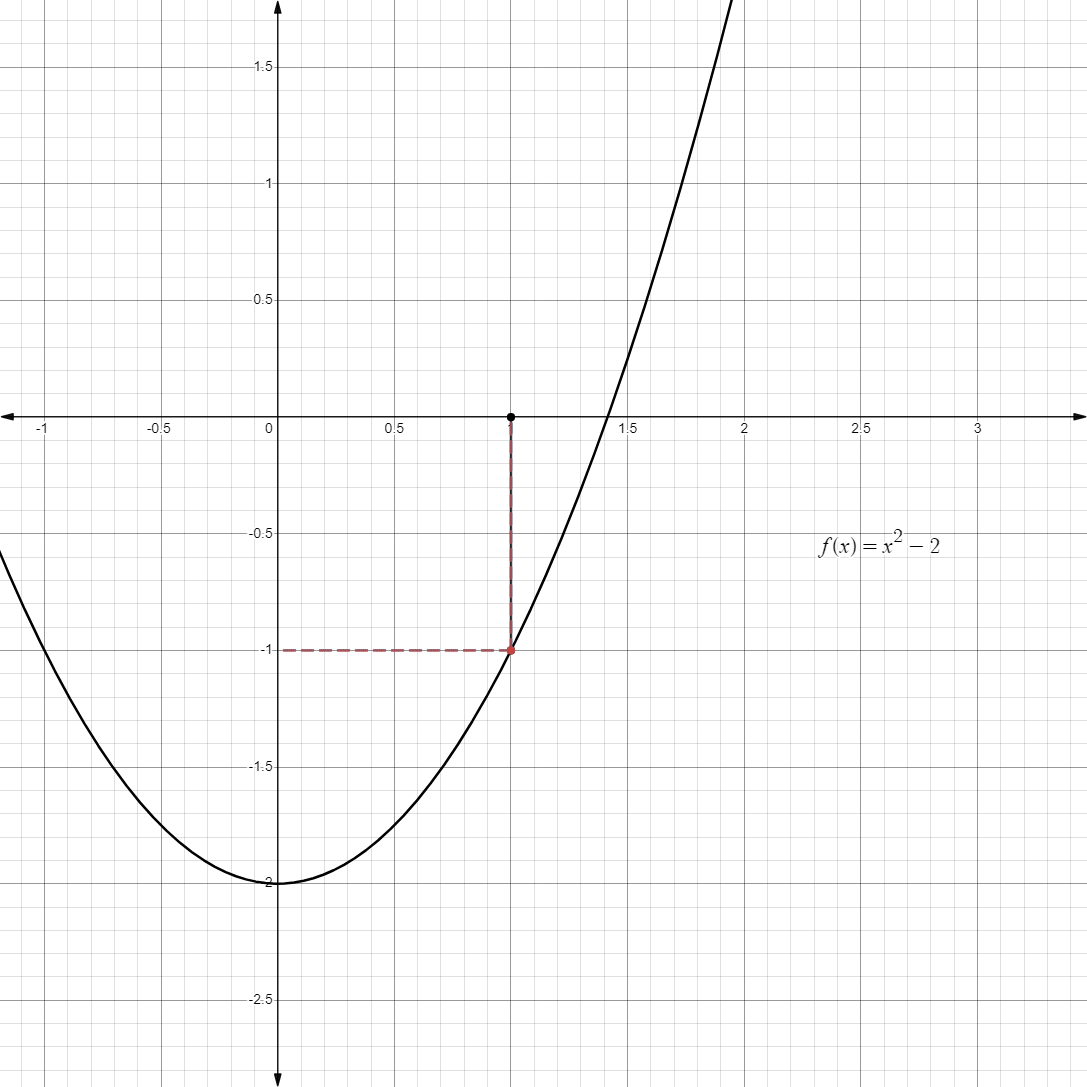
Suppose that we have the limit

We can instead use a graph to find and evaluate its limit!
- Here, we see the graph of and the value of at .

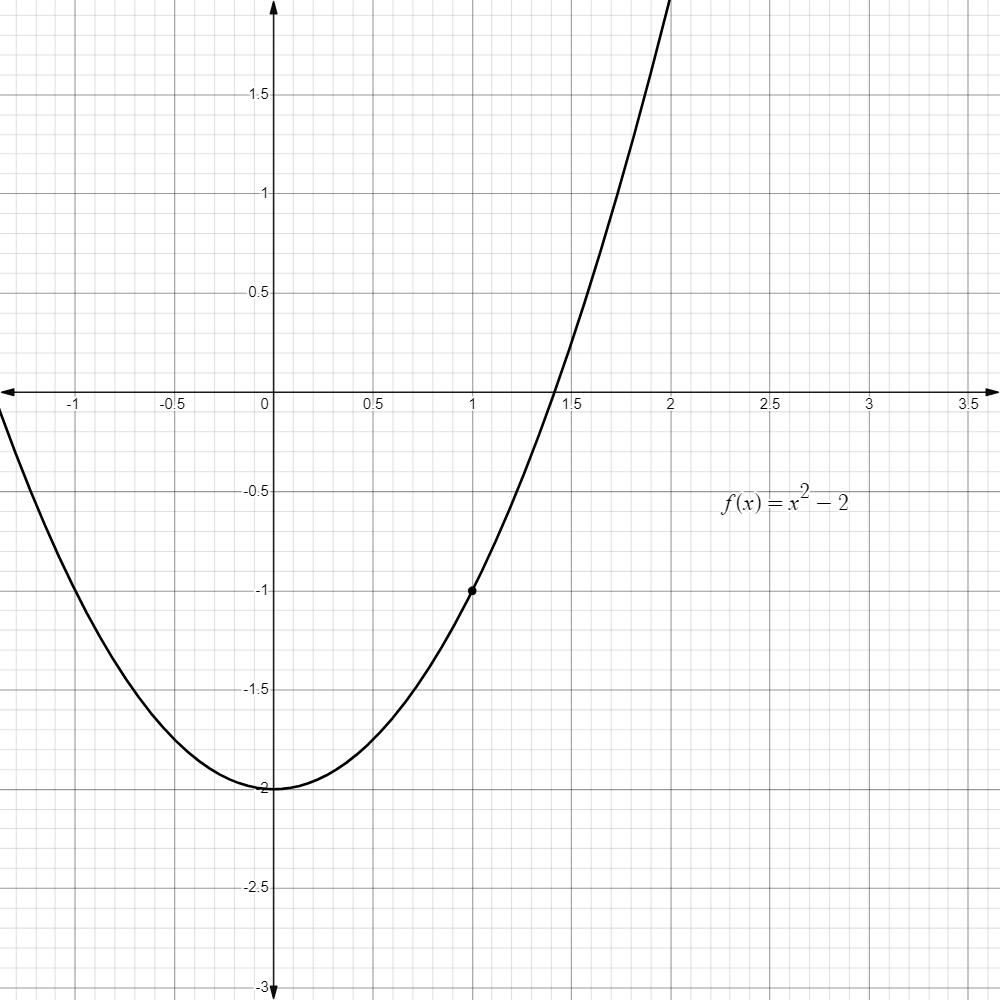
But as we approach from either side, the value closes in at .
Therefore, we can confidently say that:

You may have noticed that some limits can be evaluated by directly evaluating them.
- However, consider the limit:

If we directly evaluate it, upon further simplification, it becomes undefined.

However, if we consider approaching instead, using its graph, we get:

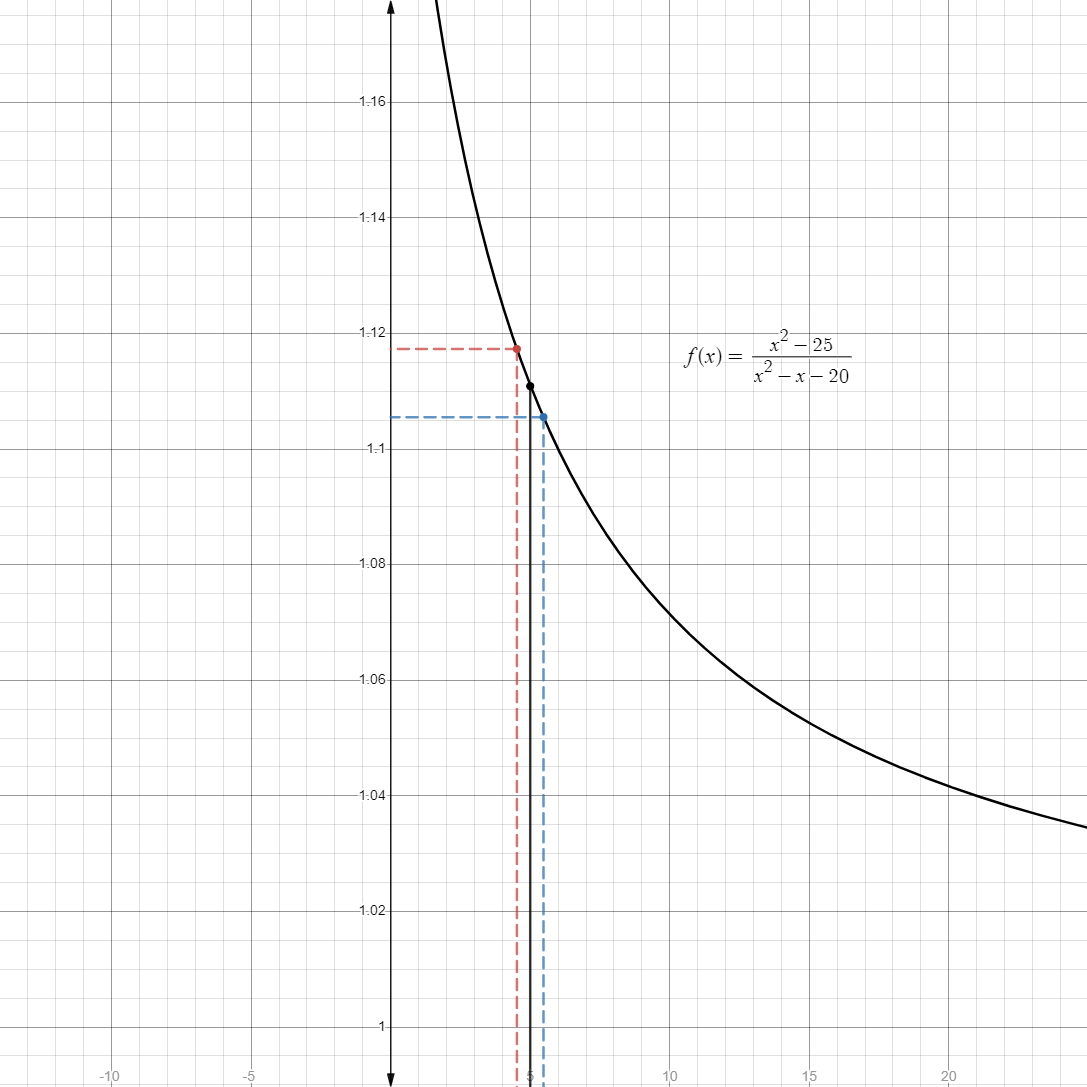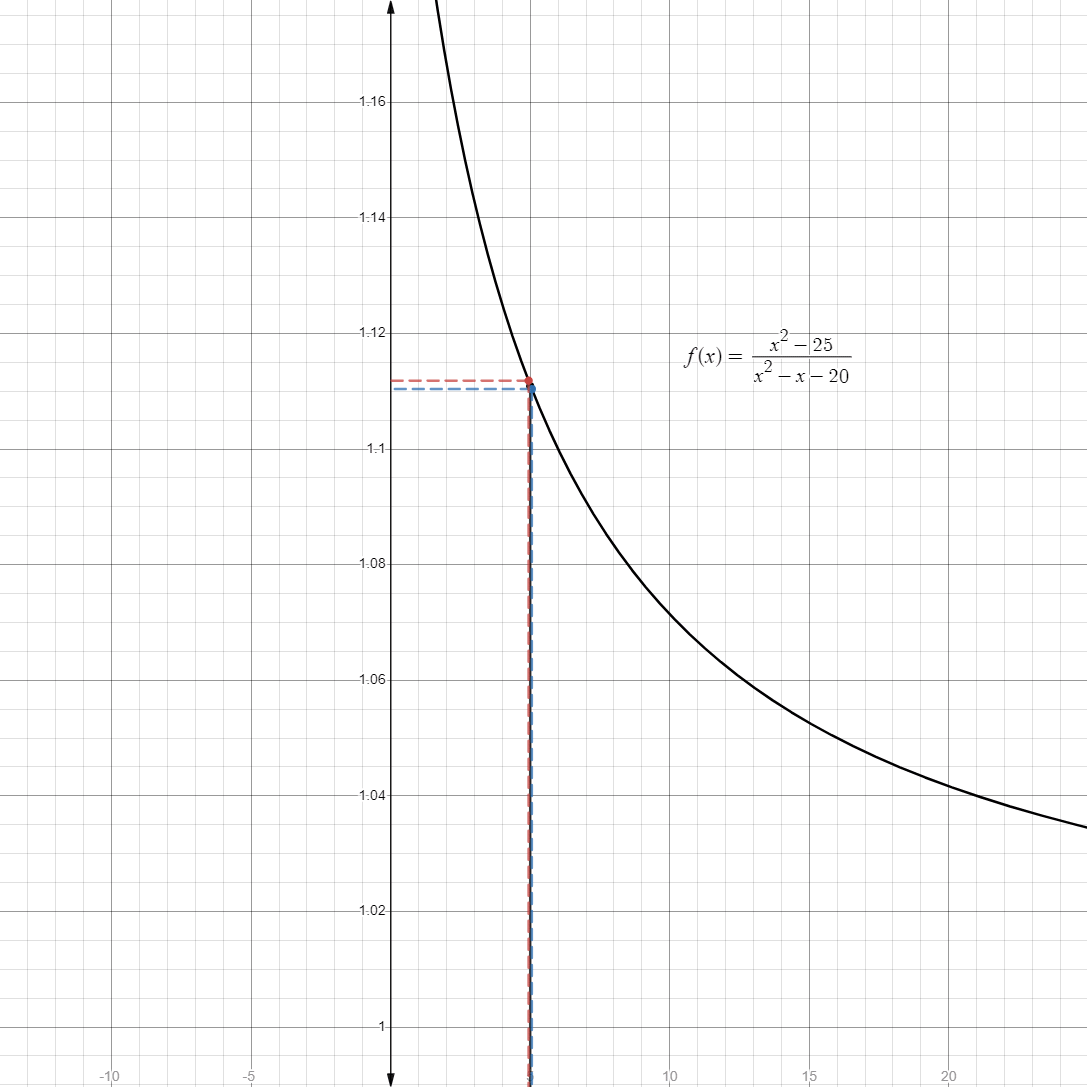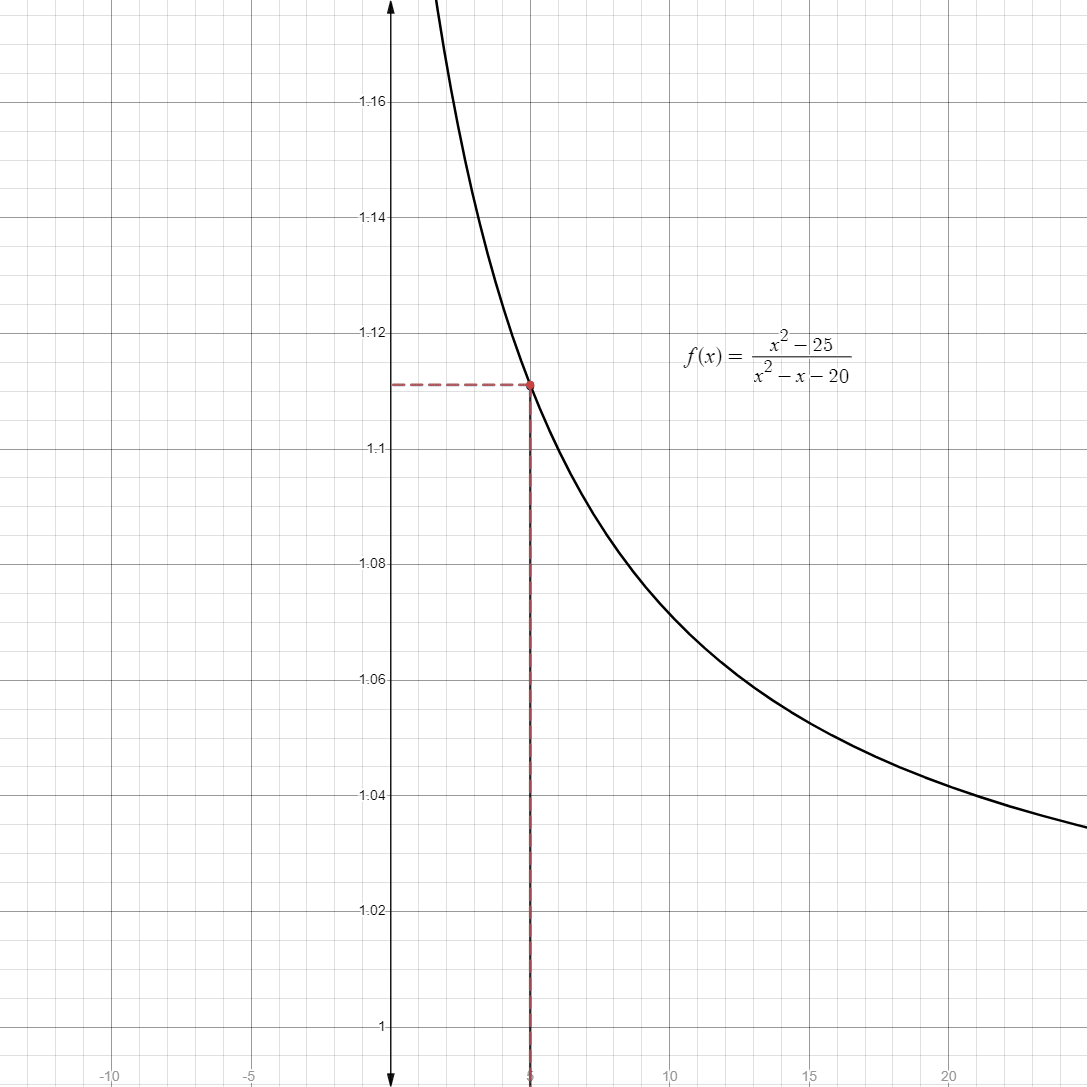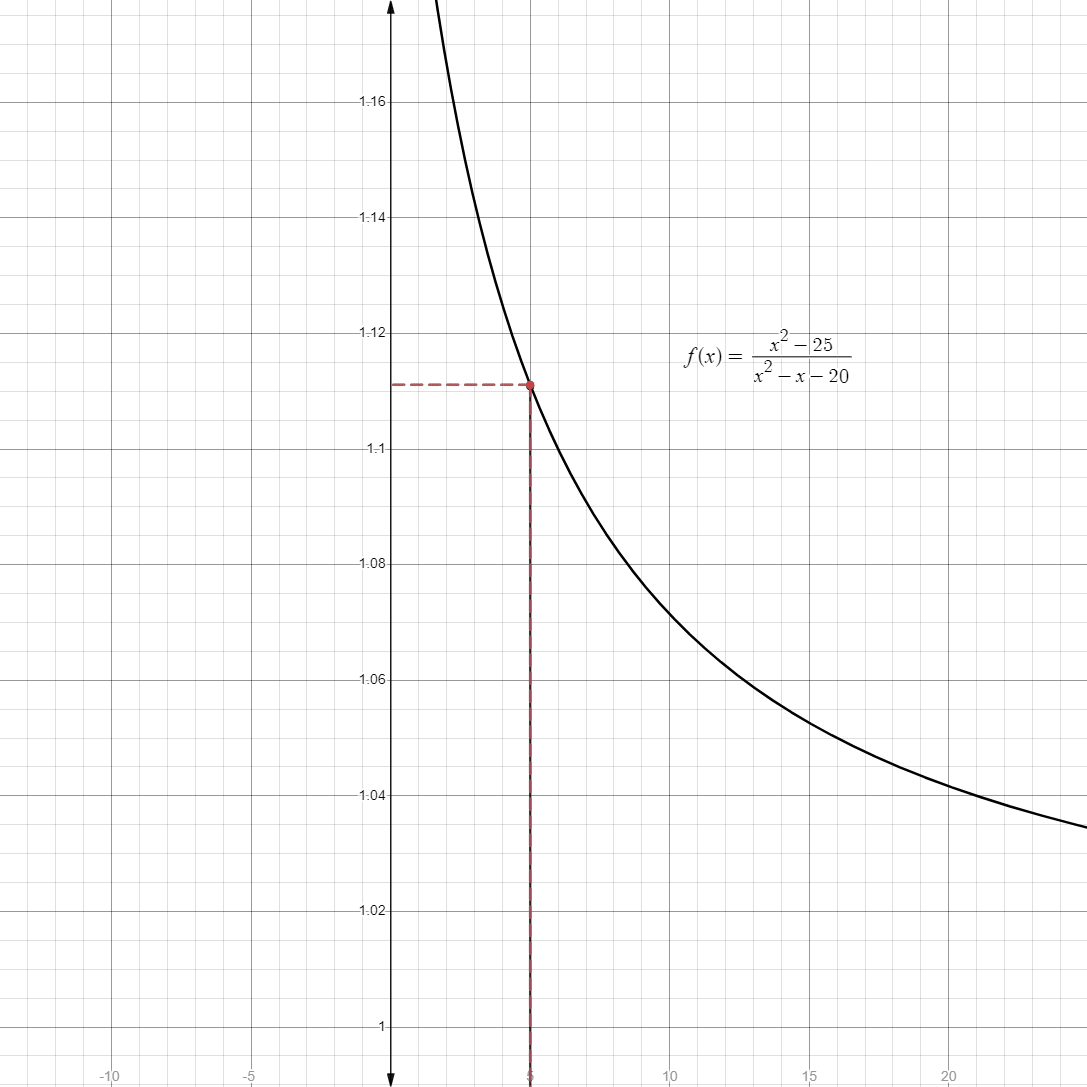
As we can see, when we approach , the limit approaches in at a single value around .
- In fact, the exact value is , which is around . Therefore:

But have you ever wondered why a limit exists yet the actual function value is undefined?
- This is because limits consider the behavior of the function around a point, not exactly at the point itself like when we evaluate the function at a point.