Inverse Functions

Objectives

• Identify the concept of an inverse function.
• Recognize when a function is invertible.
• Represent an inverse function via a table of values, an equation, or a graph.
• Evaluate an inverse function via a table of values, an equation, or a graph.
• Find the equation for an inverse of a function.
• Check your solution using the composition property of an inverse function.

What is an Inverse Function?

• We know from Key Concepts of Functions that a function is something that takes one element in the domain and pairs it to an element in the range.
  • In other words, it takes an input and pairs it to a single output.

• An inverse of a function does the opposite.
  • It takes an output and pairs it back to its input.

• In much simpler terms, it maps back a function’s output to its corresponding input.

Definition
Inverse Function

An inverse of a function maps its output values to its corresponding input values.
More specifically, it takes an element in the range of and pairs it to one element in the domain of .

Notation

• When we write an inverse of a function mathematically, we write it as:

• We pronounce this notation as “f inverse of x”.

  • Alternatively, it can also be pronounced “the inverse of f of x”

• Like in functions, we can also use other letters to represent the variable for a function’s output or input.

Important

One downside of this notation is that this does not represent a negative exponent.

When we are talking in the context of functions, this does not represent a reciprocal, but an inverse of the function itself.

Invertible Functions

Warning

The following section may be too technical.

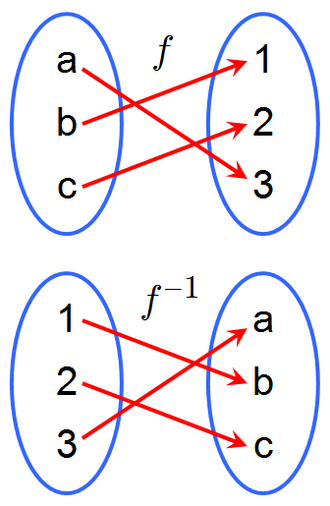
• Not all functions have an inverse.
• Consider the mapping of this function below.

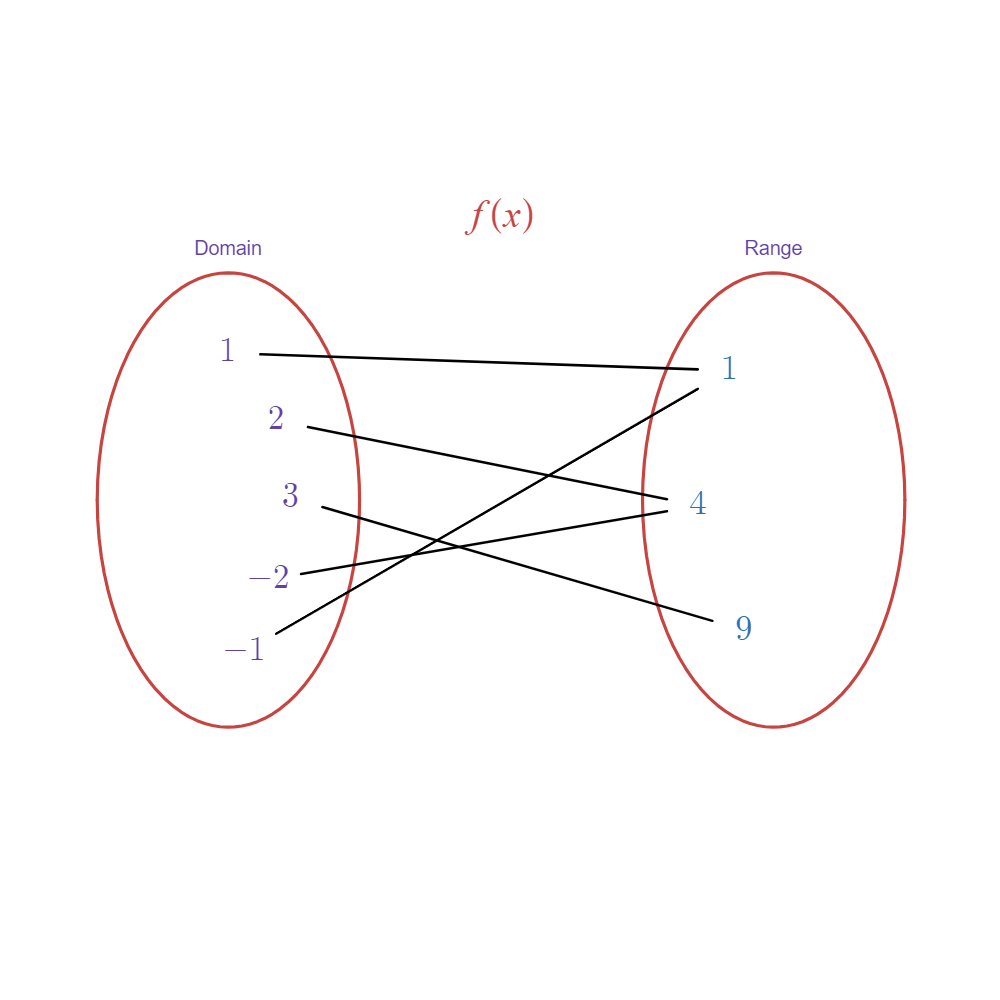
• From what we can see in this mapping, all inputs pair to a single element in the output.
  • However, we also noticed that two pair to the same output values.
• By inverting this function, or simply swapping the domain and range, we see that:

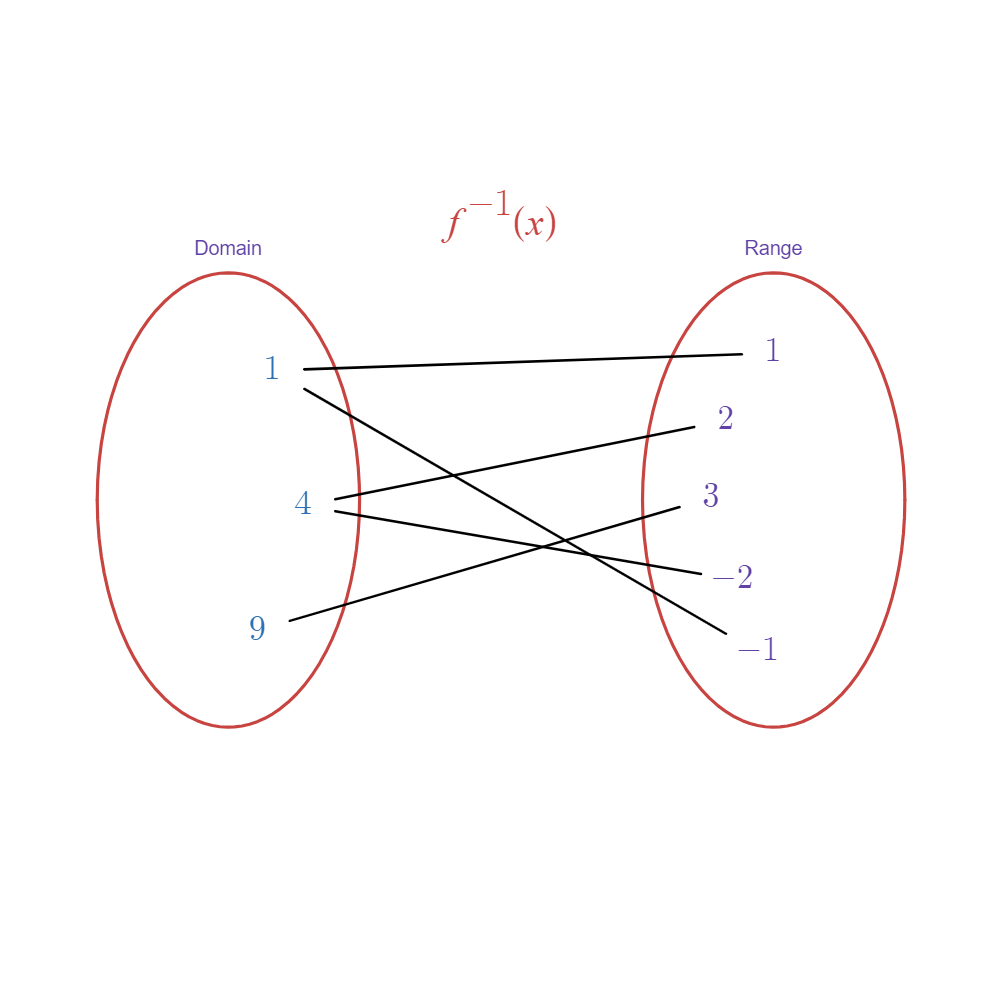
• We see that the resulting inverse is not a function.

  • Here, some inputs in the domain pair to two or more outputs in the range.

• This indicates that while a relation might be a function, its inverse might not be a function.

  • If a function satisfies this condition, the function is not invertible.

• As an another example, consider the mapping of this function below.

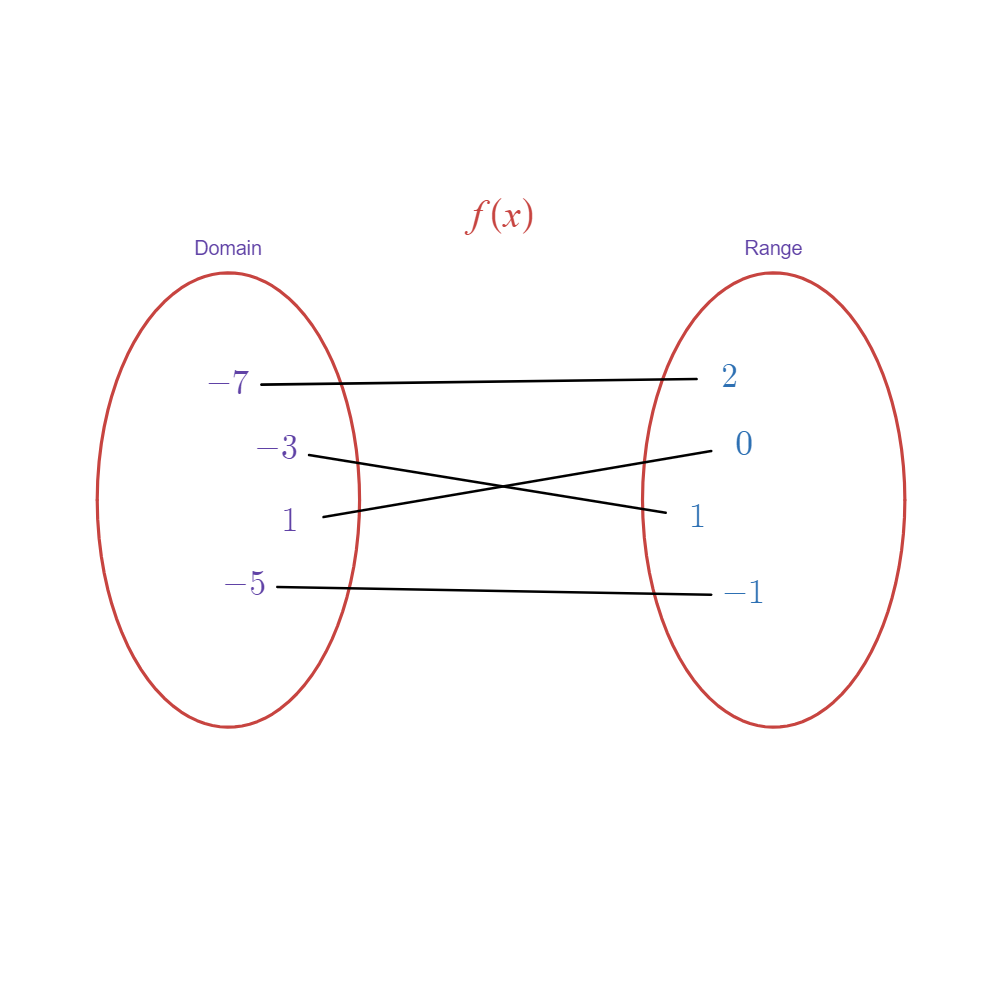
• Here, each element in the domain pairs to exactly one element in the range.
  • However, in this case, no two elements pair to the same output value.
• Inverting the mapping should give us:

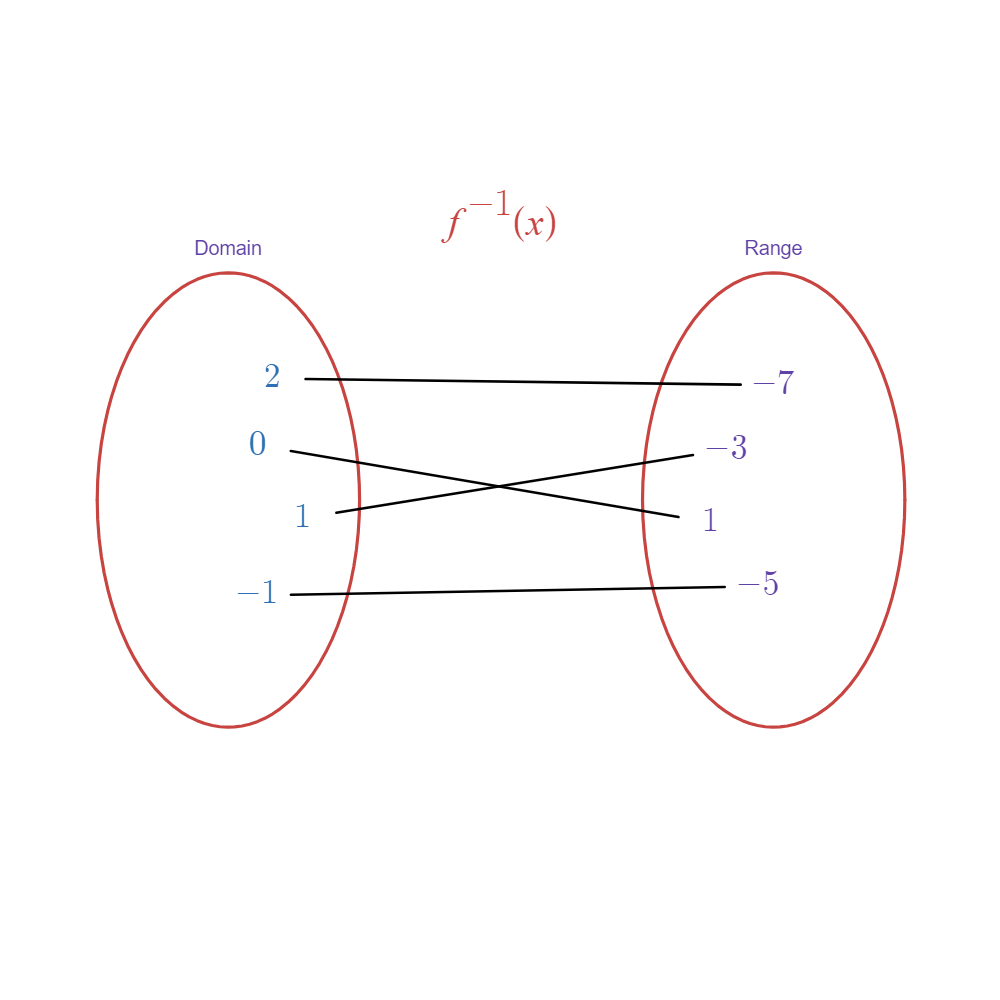
• Upon getting its inverse, the inputs of the domain now pair to exactly one output in the range.

  • Therefore, the inverse relation should also be a function, and must be invertible.

• You may notice that for a function to be invertible, all elements in the range must pair to a single item in the domain.

  • In the same page, all elements in the function’s domain must also pair to a single item in the range, as per the definition of the function.
  • Combining these two conditions, we see that for a function to be invertible, all elements in both the domain and range must only be paired once
  • Functions with this characteristic are called one-to-one functions.

Definition
Existence of an Inverse Function

Given a function :

• A function is one-to-one if all elements in the range pair to exactly one element in the range.
• A function is invertible if the function has an inverse.

If is one-to-one, then must be invertible, and therefore, has a unique inverse.

Worked Example
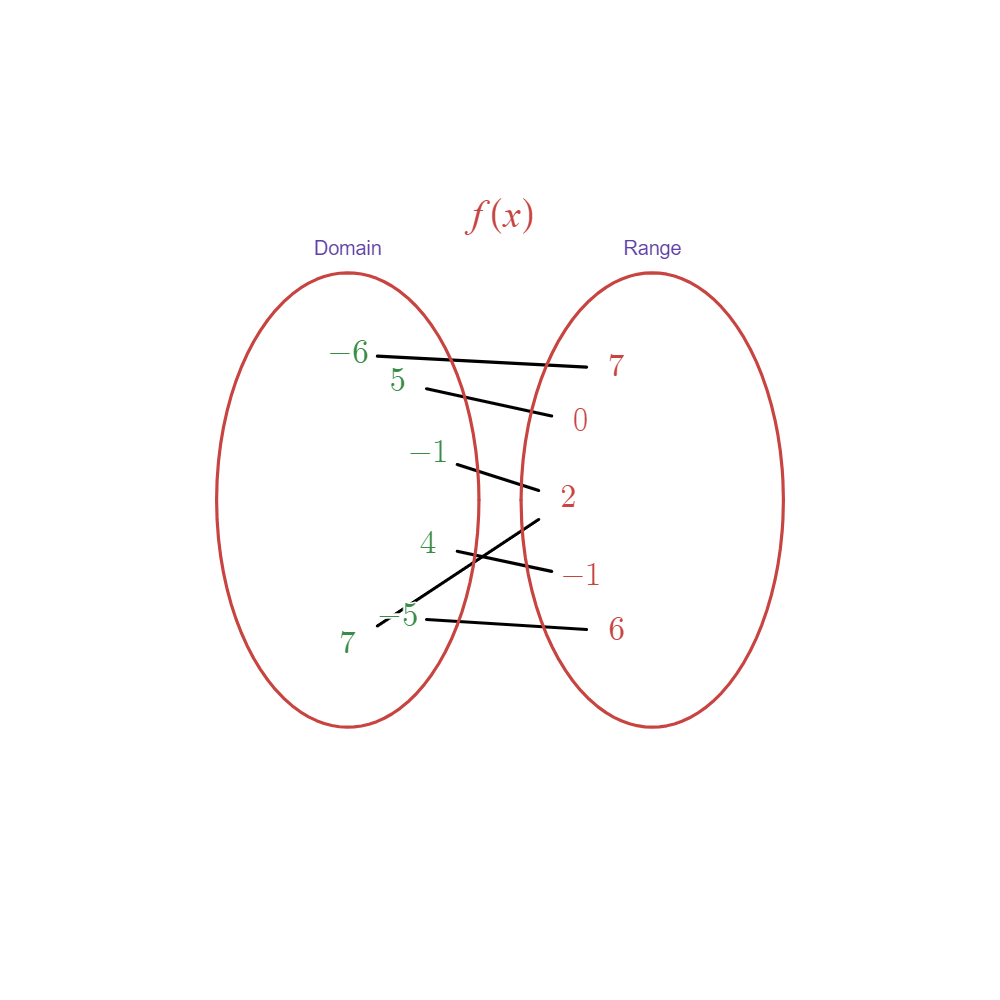
Proving if a Table of Functional Values is Invertible

Let be defined as the table of values described below.

Determine if the function is invertible or not.

Solution

We can try to solve this by taking at look at each pairing to see if they are one-to-one

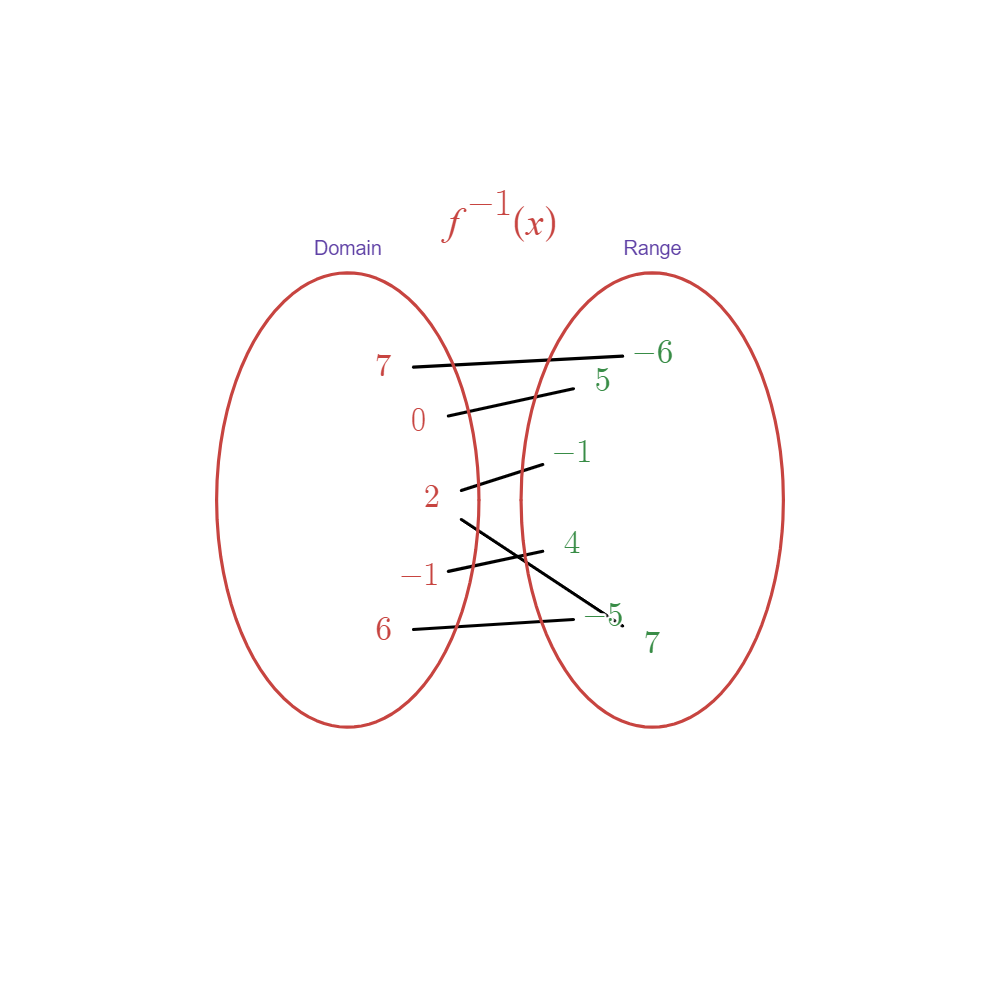
Since both and both pair to , then this function is not one-to-one, and henceforth, not invertible.

We can also see this by drawing a mapping of each table of values.

Inverting it should give us a relation that is not a function.

The inverse cannot be a function so it has no inverse.

Horizontal Line Test

• Since one-to-one functions are invertible, then no two different inputs should have the same output.
• For instance, take a look at the graph of .

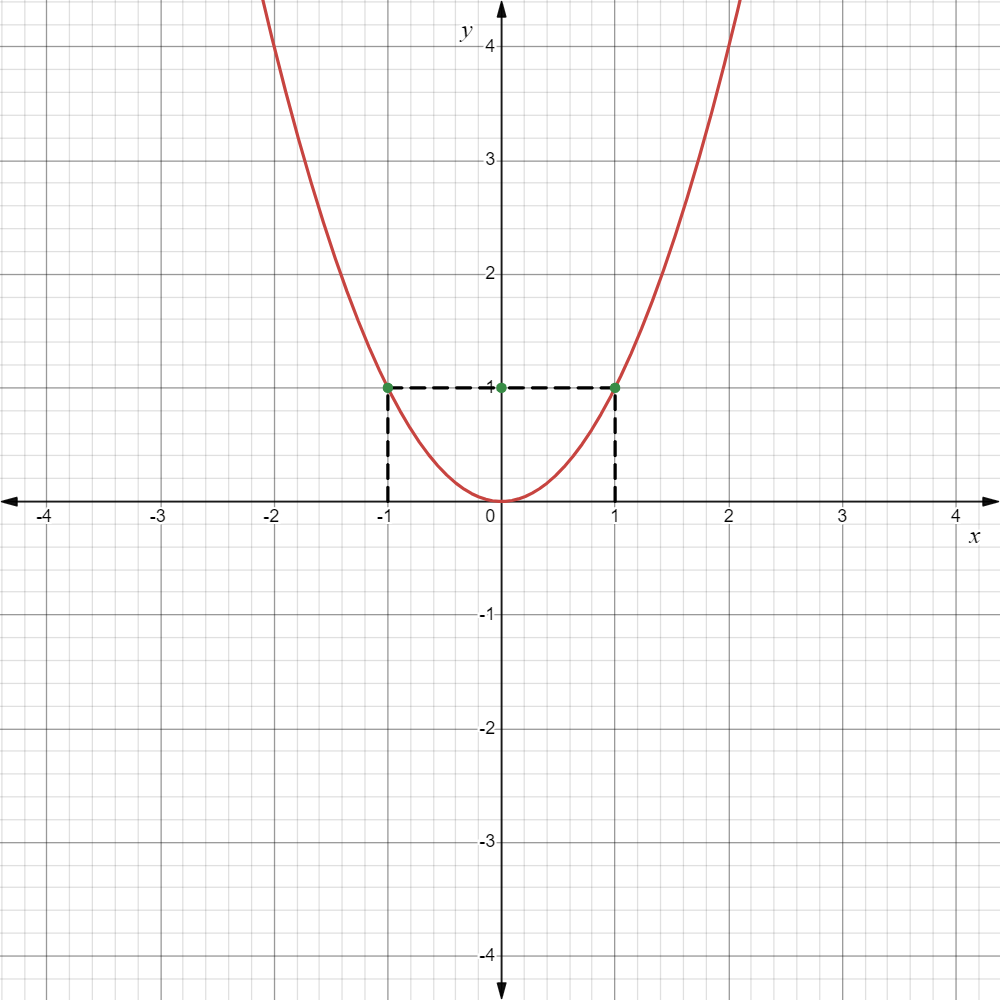
• As we can see, both the input values and map to .

• Therefore, this is not a one-to-one function and therefore not invertible.

• As you may have noticed, if we graph the points where two or more input values map to the same output, they seem to align horizontally.

• From this, we can say that if a horizontal line intersects the graph of a function for more than two points, then the function is not one-to-one.

Definition
Horizontal Line Test

Given a graph of any function , if a horizontal line placed anywhere in the graph crosses or intersects the graph for more than two points, then the function is not one-to-one, and therefore not invertible.

Worked Example
Using the Horizontal Line Test

Below is the graph of .
Determine if the function is invertible or not.

Solution

No matter where we place the horizontal line, it still does not intersect for more than two points. Therefore, this function has an inverse.

Evaluating Inverse Functions

• Now that we know that some functions may or may not have an inverse, we can consider how to exactly evaluate them.
• Suppose that is defined as this table of functional values.

• What do you think will will be?

  • What this is saying is: “what input value will make the function equal to “?
  • From the table, we can see that if , .
  • Therefore,

• How about ?

  • Since we can see that the value of is , therefore is .

Worked Example
Evaluating Inverse Functions from a Table of Values

Consider the following table of values below.

Evaluate the following expressions.

Solution

Looking at the table of values, we can evaluate the first two by looking what output values values pair with and .

To evaluate an inverse function, we just ask: “what input value pair to the value inside the function?” Looking at the table, we get the values:

• One way we could also do this is we can swap the input and output values.
• Then we rename into .

• By swapping the input and output values to form the inverse, we can say that the range of is the domain of , and the domain of is the range of .

• We can also evaluate inverse functions using a graph.

• Consider the following function:

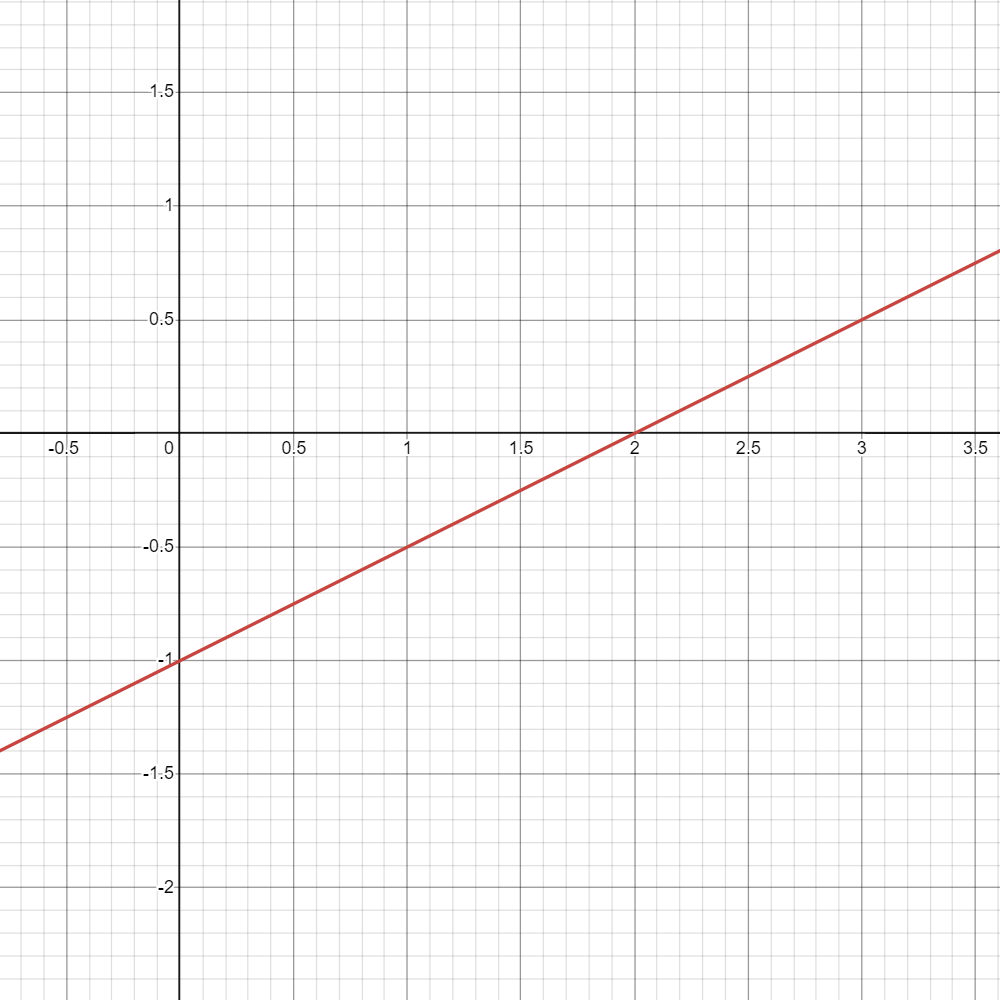
• From this graph, what do you think is?
  • Since is , then if should be .

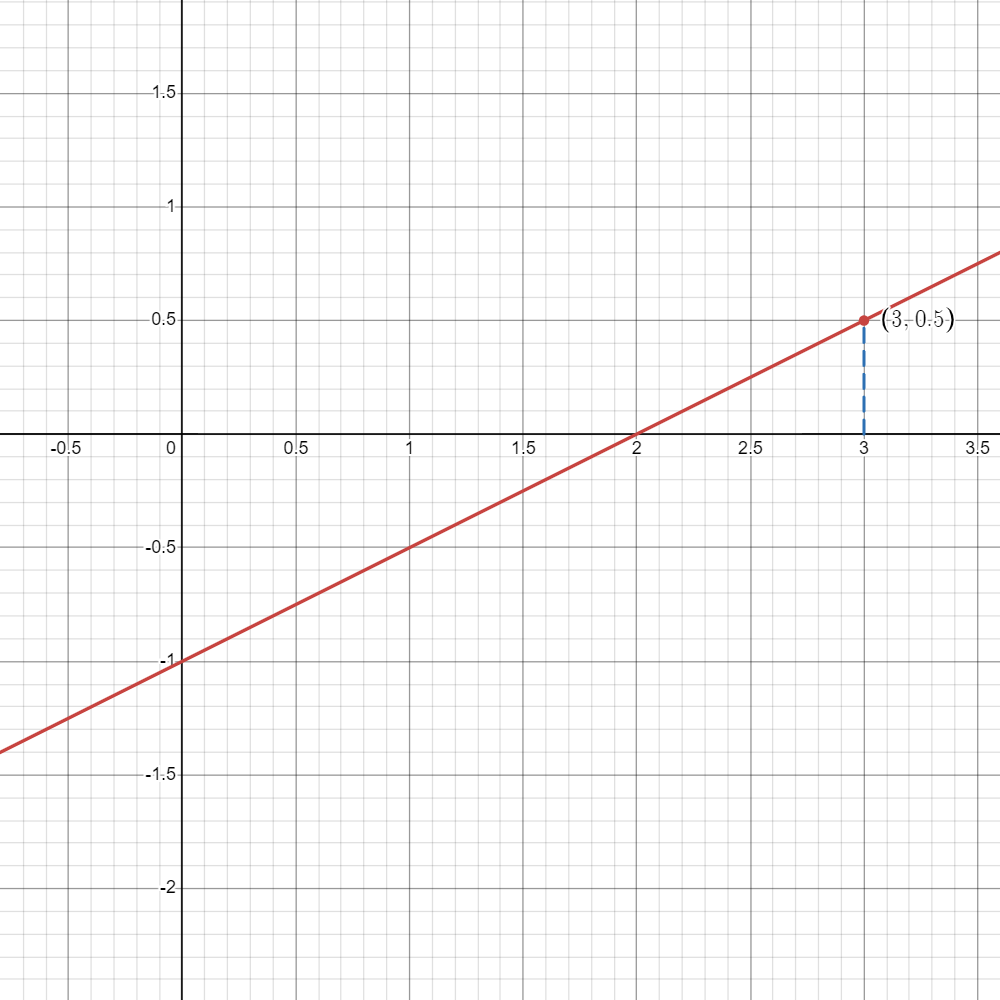
• How about when ?
  • Sine we see that , it also follows that

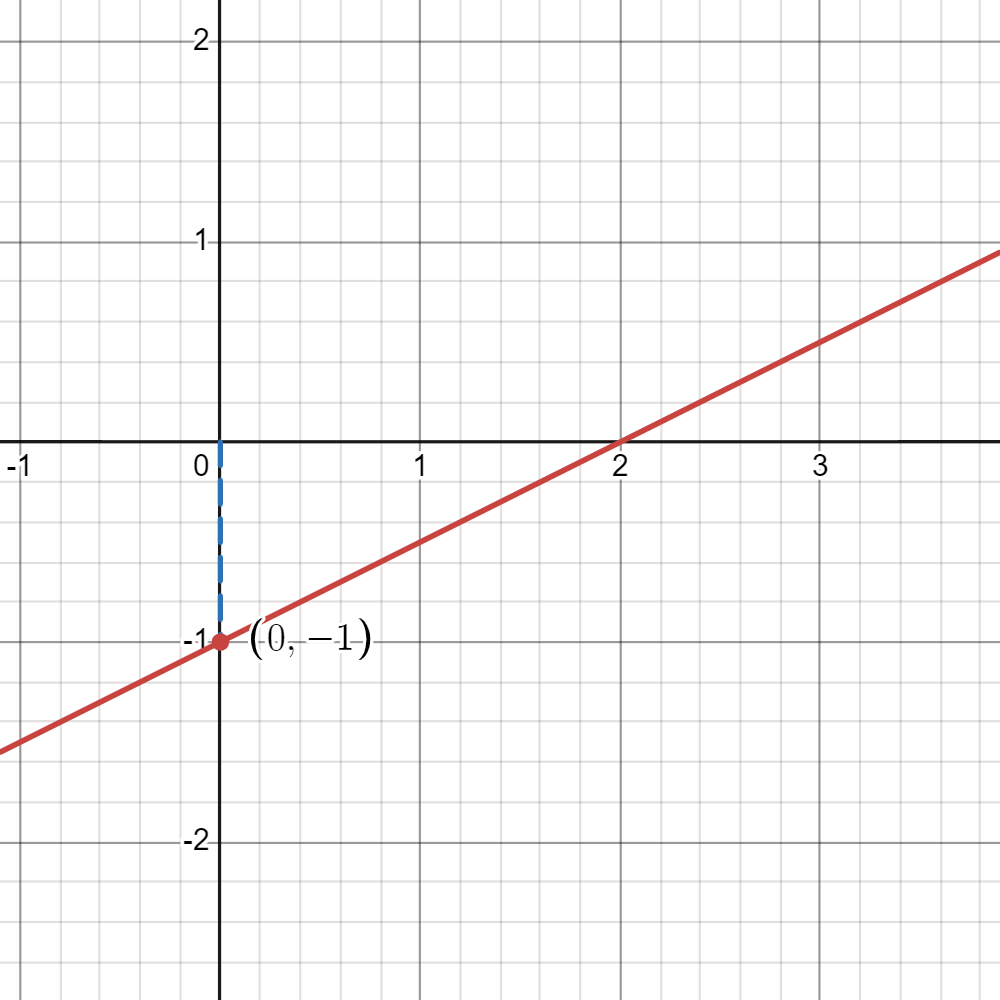
Problem
Evaluating Inverse Functions using a Graph

Use the graph below to evaluate the following:

• We can also evaluate an inverse function in equation form.
• Suppose that we want to find when .
  • What this is saying is what number will make the function equal to ?
  • We can then set up an equation.

• Solving this equation gives us:

• Therefore, is .

Worked Example
Evaluating Inverse Functions in Equation Form

Find if

Solution

Since we are evaluating , what we are trying to find is when the function equals . Now that we know this, we can set up an equation.

Therefore, .
We can check this by evaluating and let’s see if it equals .

Composition of Inverse Functions

• We now know that a function maps an input to its output, while an inverse function maps the output back to its original input.
• For example, suppose that we have the function and its inverse
  • What would the look like?
  • Well, as discussed in Composition of Functions, we would evaluate the inside expression first before the outside.
  • Using our analogy of a machine, this would look like:

• What this means is that the function maps to , and then applying the inverse maps back to our original input .
  • Essentially, if we put something in a function, then put the output of that to its inverse, then it will give us our original input .
• In general, we get the property:

Definition
Properties of Inverse Functions

Given an invertible function , the composition of and its inverse will always be equal to:

• This can be helpful in proving whether if two functions are both inverses of one another.

Worked Example
Proving if Two Functions are Inverses

Let:

Prove if is the inverse of .

Solution

First, we know that composing a function and its inverse should give its original input .

If is the inverse of , then they should satisfy the condition from above.

We substitute our first.

Then our ,

Simplifying this gives us

Finding an Expression for an Inverse Function

• In a related case, when we use units for temperature, we express it in either degree Celsius or degree Fahrenheit.
• But consider this, what if we wanted to express our units from Celsius to Fahrenheit?
  • We may be able to use the formula below:

• So if a bowl of cold soup has a temperature of , in Fahrenheit, it would be:

• Therefore, is equivalent to in Fahrenheit.
• But question this, what if we start from the other way around: from Fahrenheit, then convert it to Celsius? Would there such be a formula for this type of conversion?
  • Indeed there is, and in order to convert from Fahrenheit to Celsius, we use the formula:

• Using the formula to convert should give us:

• But why is this relevant?
  • It turns out that the formulas that we use for converting from degrees Celsius to degrees Fahrenheit and vice versa are inverses of one another.
  • Therefore, we can express the formula for converting degrees Celsius to degrees Fahrenheit as:

• One question that we may ask is: “How exactly did we find the formula for converting from Fahrenheit to Celsius?”
  • Since both of them are inverses, then from the definition of an inverse, we can express our original formula first as an equation.

• Then, we solve for instead.

• The resulting expression for looks like the same as our formula for converting Fahrenheit to Celsius.

• This method is a way to find an expression for the inverse of a function.

• For instance, take the function .

  • To find its inverse, simply express it in equation form.
  • This can be done by replacing with an another variable like

• Then, instead of solving for , we solve for .
  • Most often in some books, we swap the variables first often to indicate that the domain and range is swapped.

• The resulting expression for should be the inverse of our original function .
  • We can now replace with our notation for the inverse .
  • Therefore, the inverse of is:

General Instructions
Finding the Inverse of a Function

To find the inverse of a function, consider these steps:

• Express the function in equation form in terms of
• Swap the and variables.
• Solve for .
• Replace with the notation for the inverse .

Worked Example
Finding the Inverse of a Linear Function

Find the inverse of the function

Solution

To find the inverse, we first express it in equation form, then we swap the variables

Then, we solve for .

Therefore, the inverse of is .