Objectives
- Define a one-sided limit.
- Determine the conditions for the existence of a limit
One-sided Limits
- When we approach a point in a function, we can approach it from two separate directions: from the left and from the right.
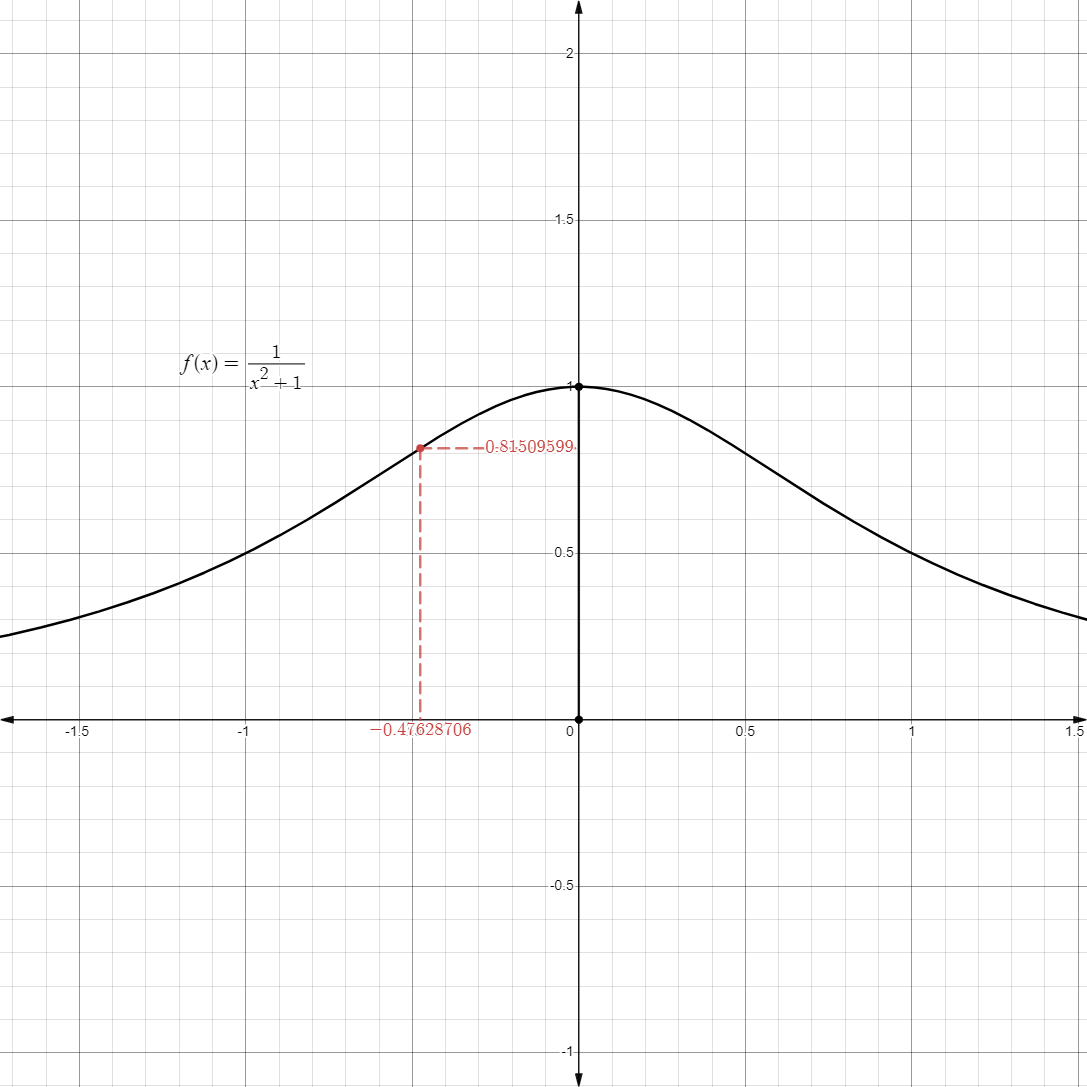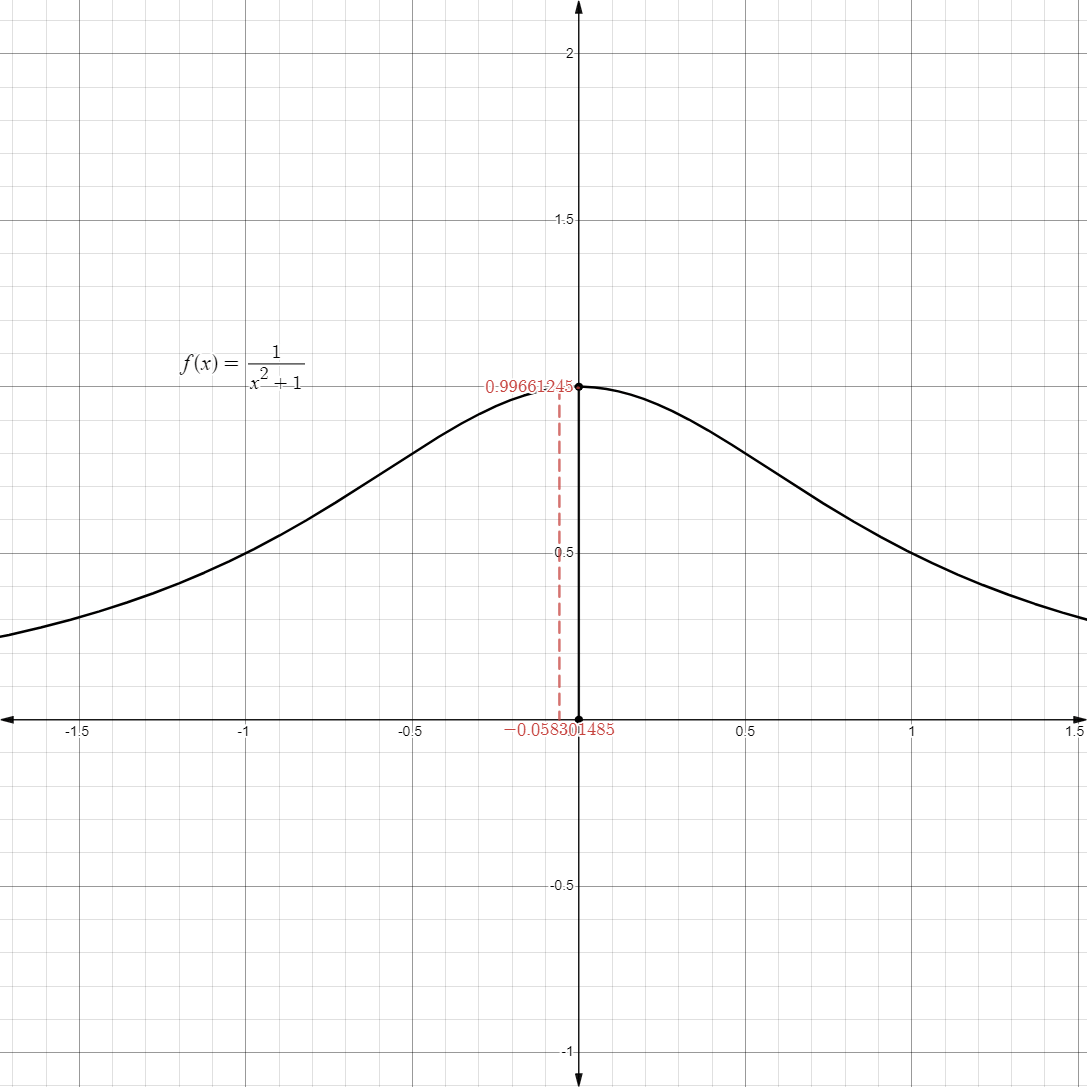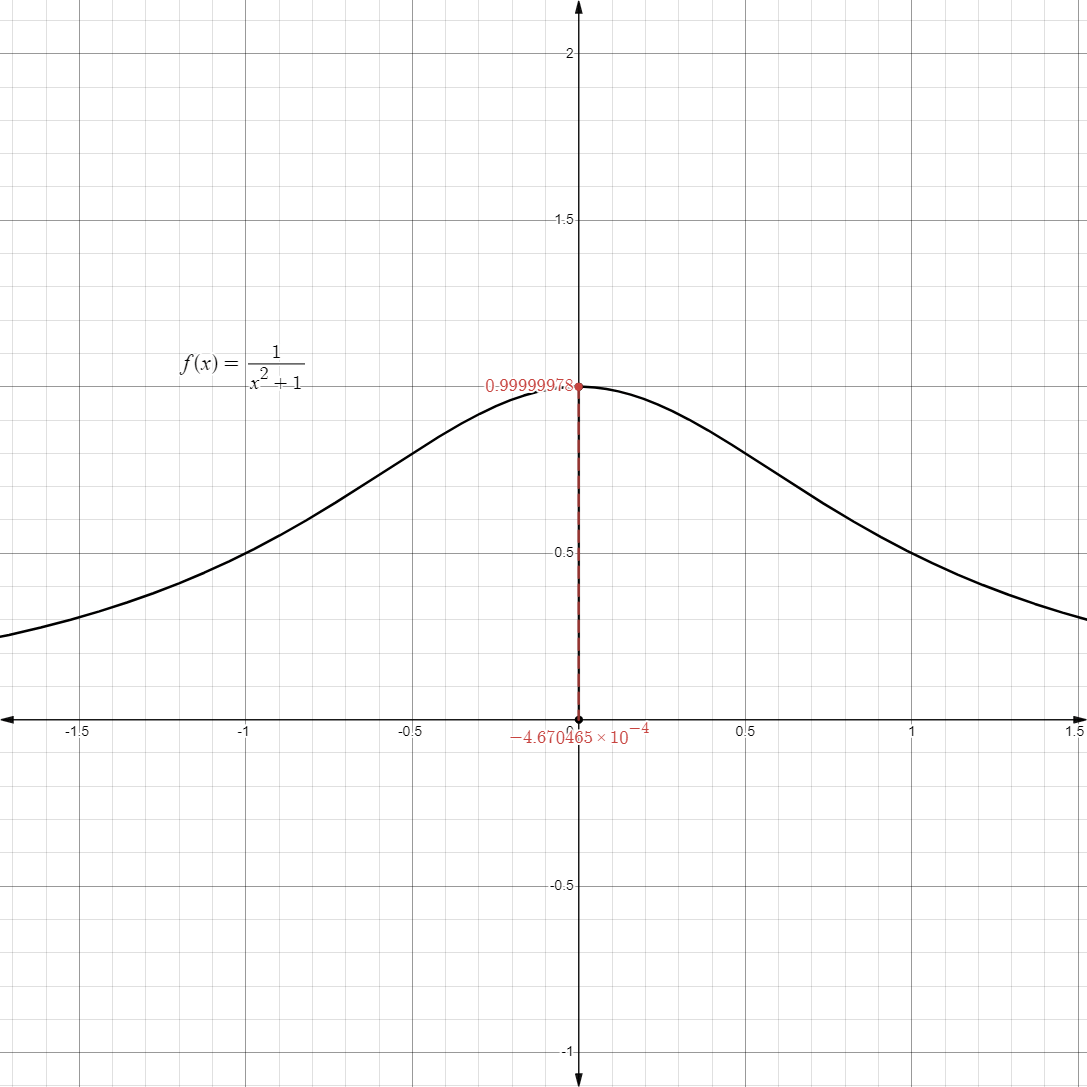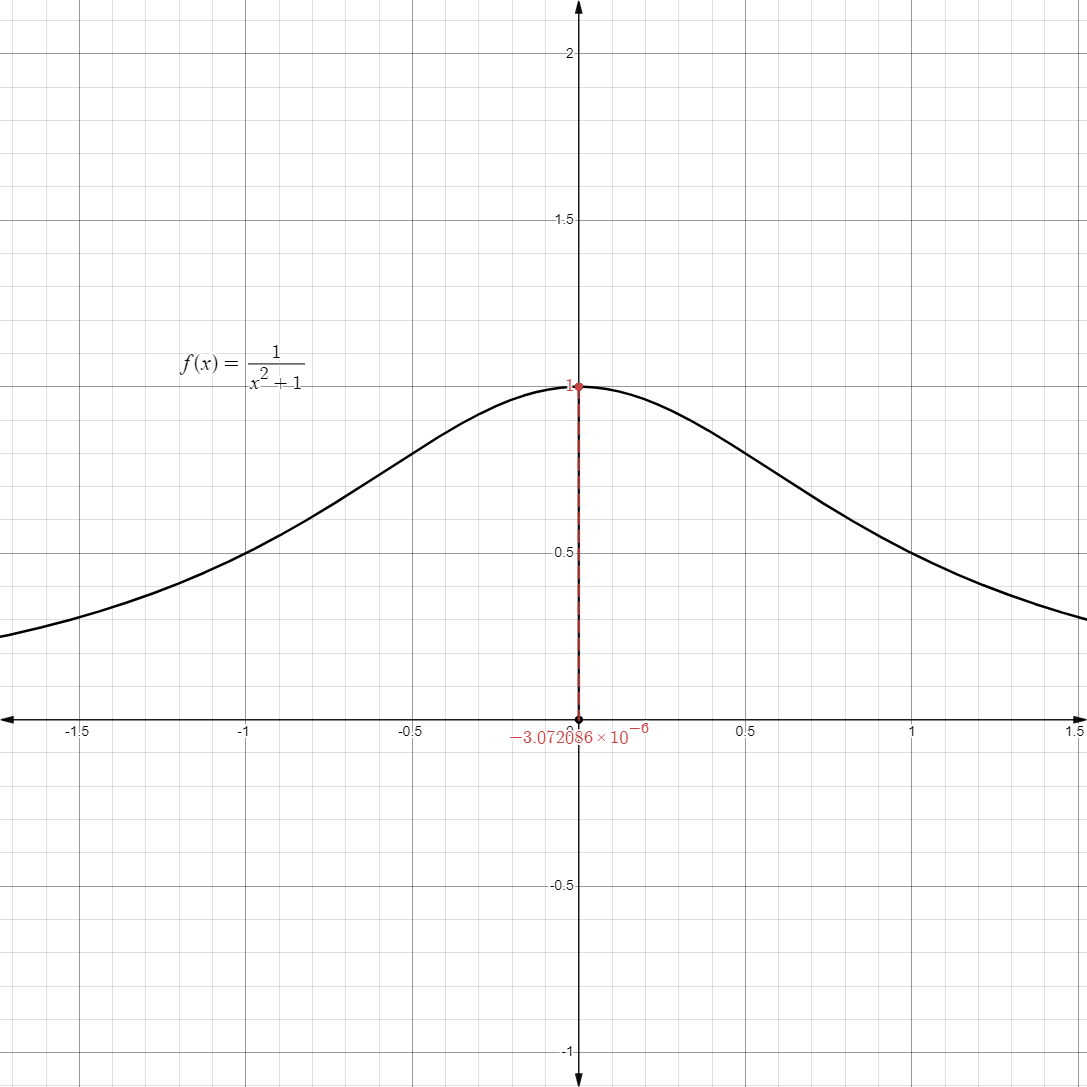
- For example, let us consider the following limit below:
- When approaching the point
, we can use values that are greater than itself.
- In a graph, it might look something like this:

- This is also called a limit from the positive direction or limit from the right.
- Likewise, we can also approach
coming from values less than itself
- In a graph, it might look something like this:
- This is also called the limit from the negative direction or a limit from the left.
Definition
One-sided LimitsA one-sided limit is a limit approaching a point from a single direction.
- A limit from the right or a limit from the positive direction approaches the point
with values greater than itself. This is expressed as:
- A limit from the left or a limit from the negative direction approaches the point
with values less than itself. This is expressed as:
Existence of a Limit
- Oftentimes, a limit of a function at a point may note even exist.
- For example, consider the limit of the following function.
- If we try to approach the point from the right, we get that the limit is equal to
.

- However, if we try to approach the point from the left, we get that the limit is equal to
.
| ![[oslim-4.gif | 600]] |
- We see that when we approach them in either side, the limits from both directions don’t match.
- Therefore, this limit does not exist.
Definition
Existence of a Limit: One-Sided Limits Do Not MatchGiven any function
, if the one-sided limits at a point do not match, then the limit of at does not exist. In other words, if:
then,
does not exist. On the other hand, if both one-sided limits match and it is equal to some real number
, then the limit of at is . In other words, if
then,
.
- One other way that the limit does not exist is when the values seem to get bigger and bigger as it gets closer and closer towards a particular point.
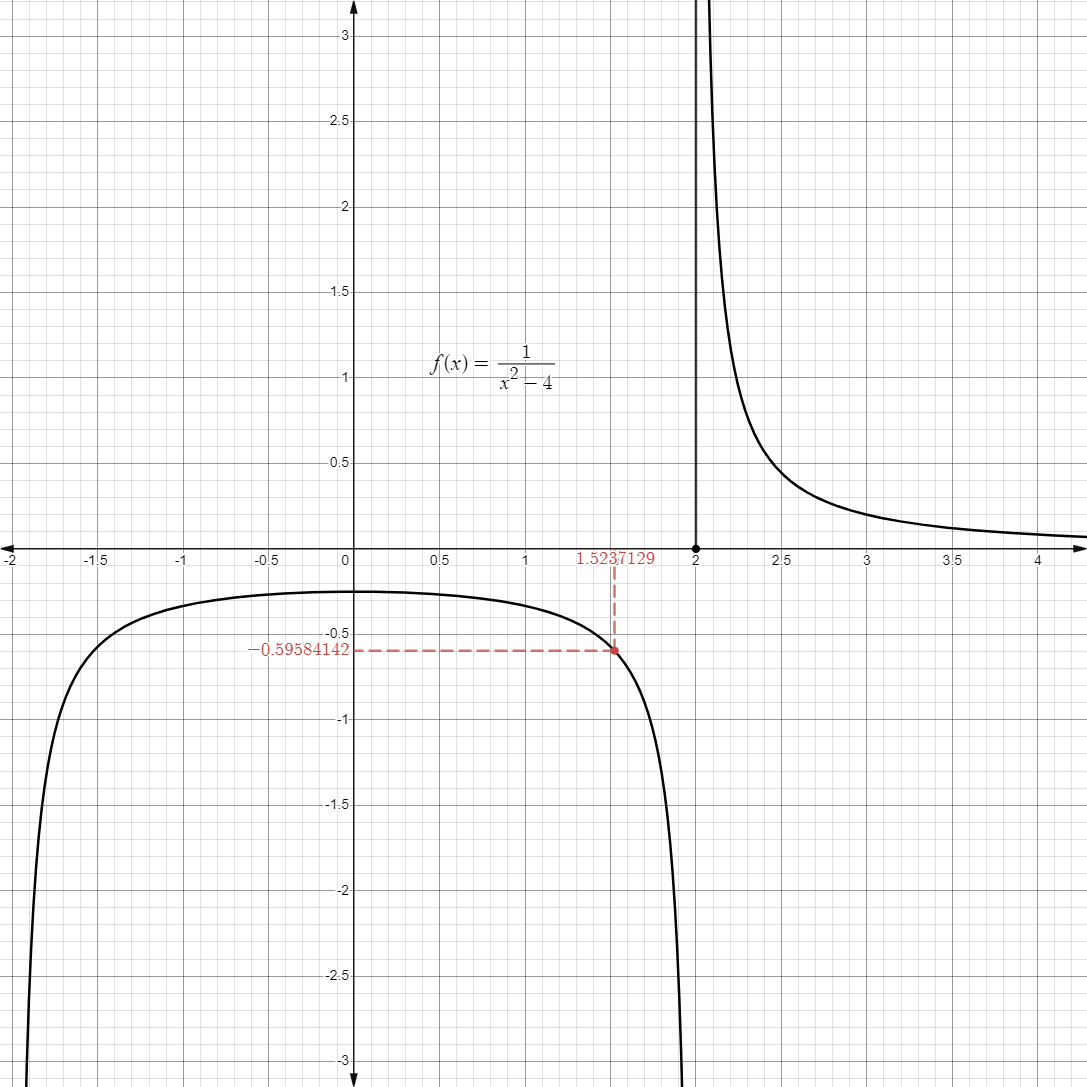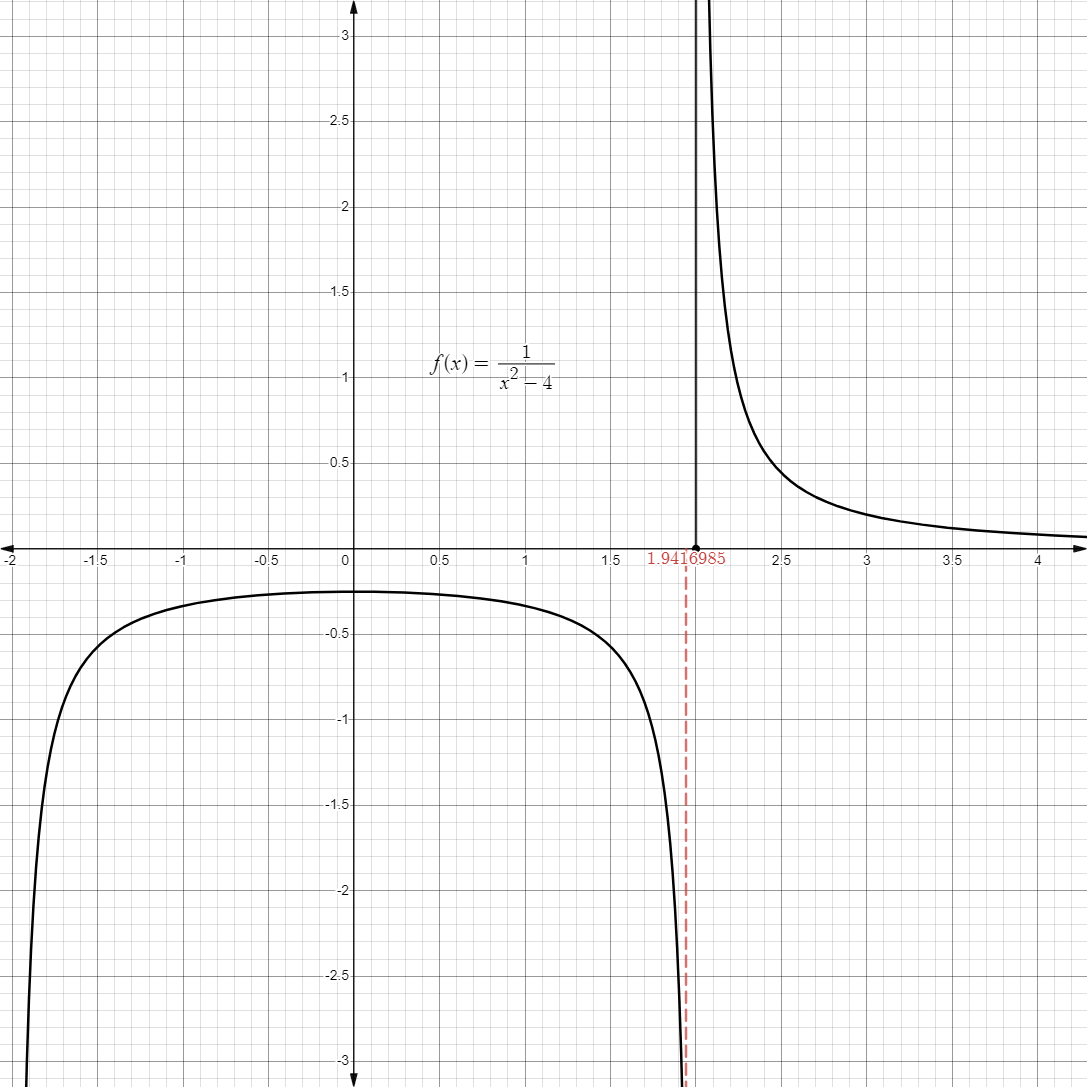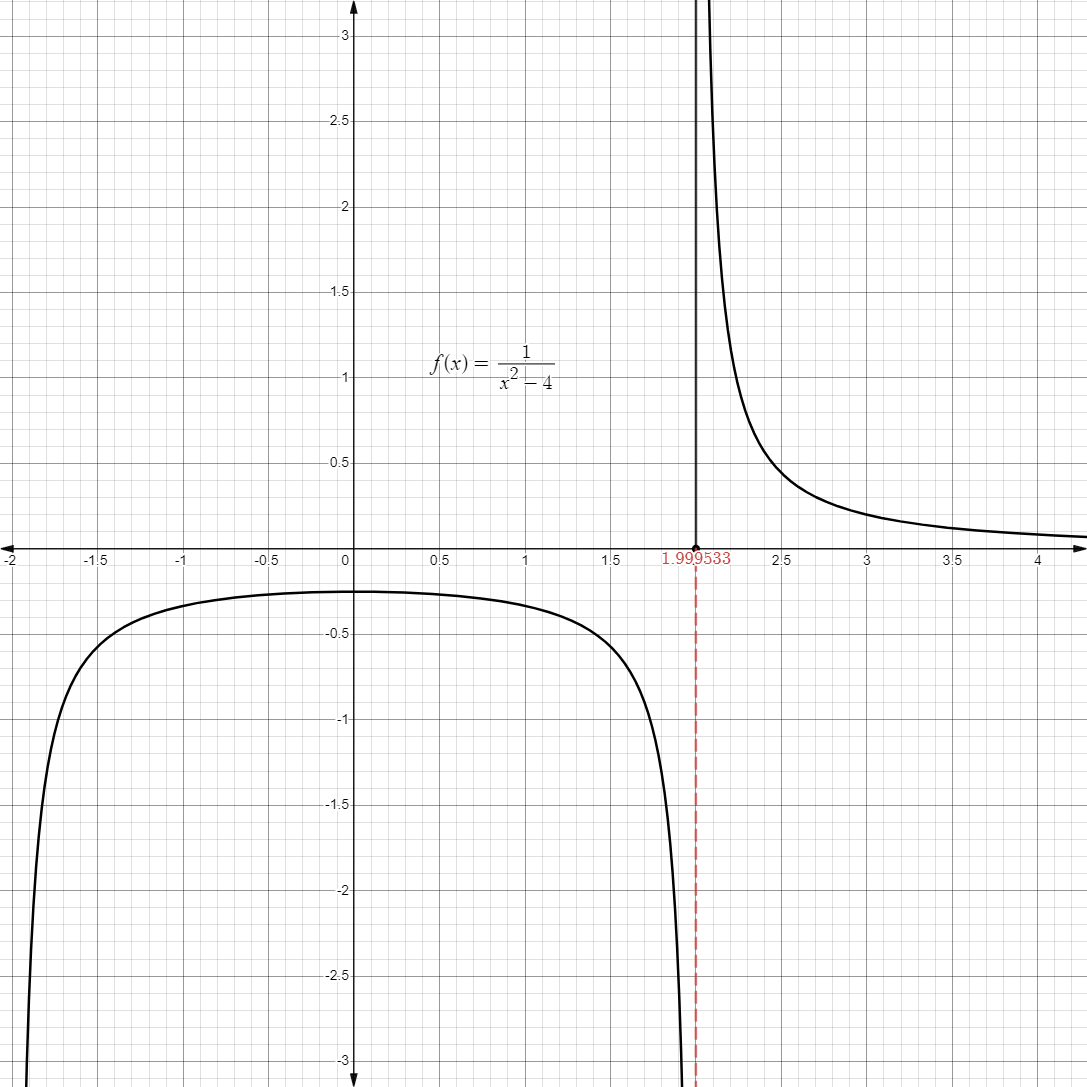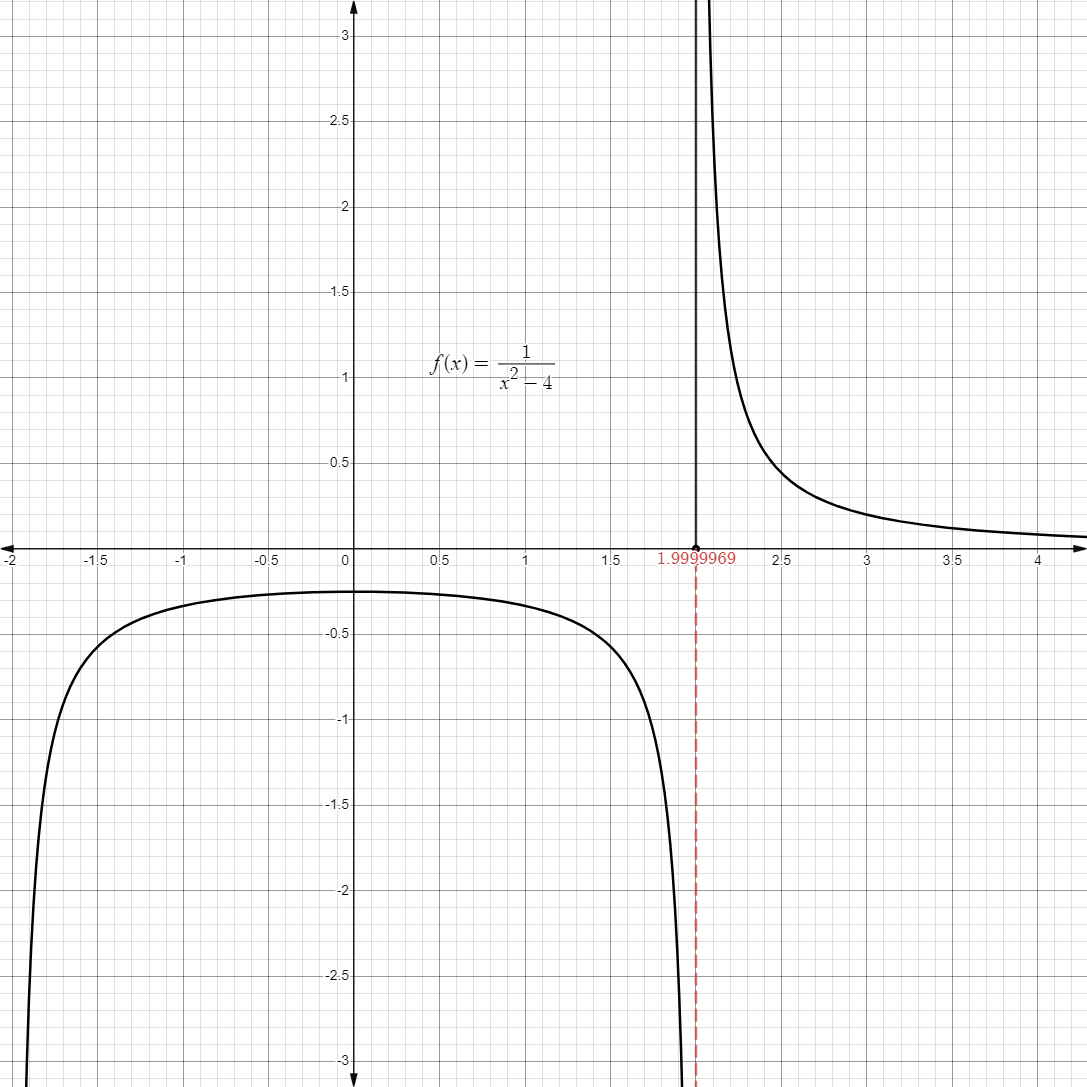
- For example, consider the limit below:
- For example, if we approach
from the right, starting from , we get:
- Graphically, it may look like this:
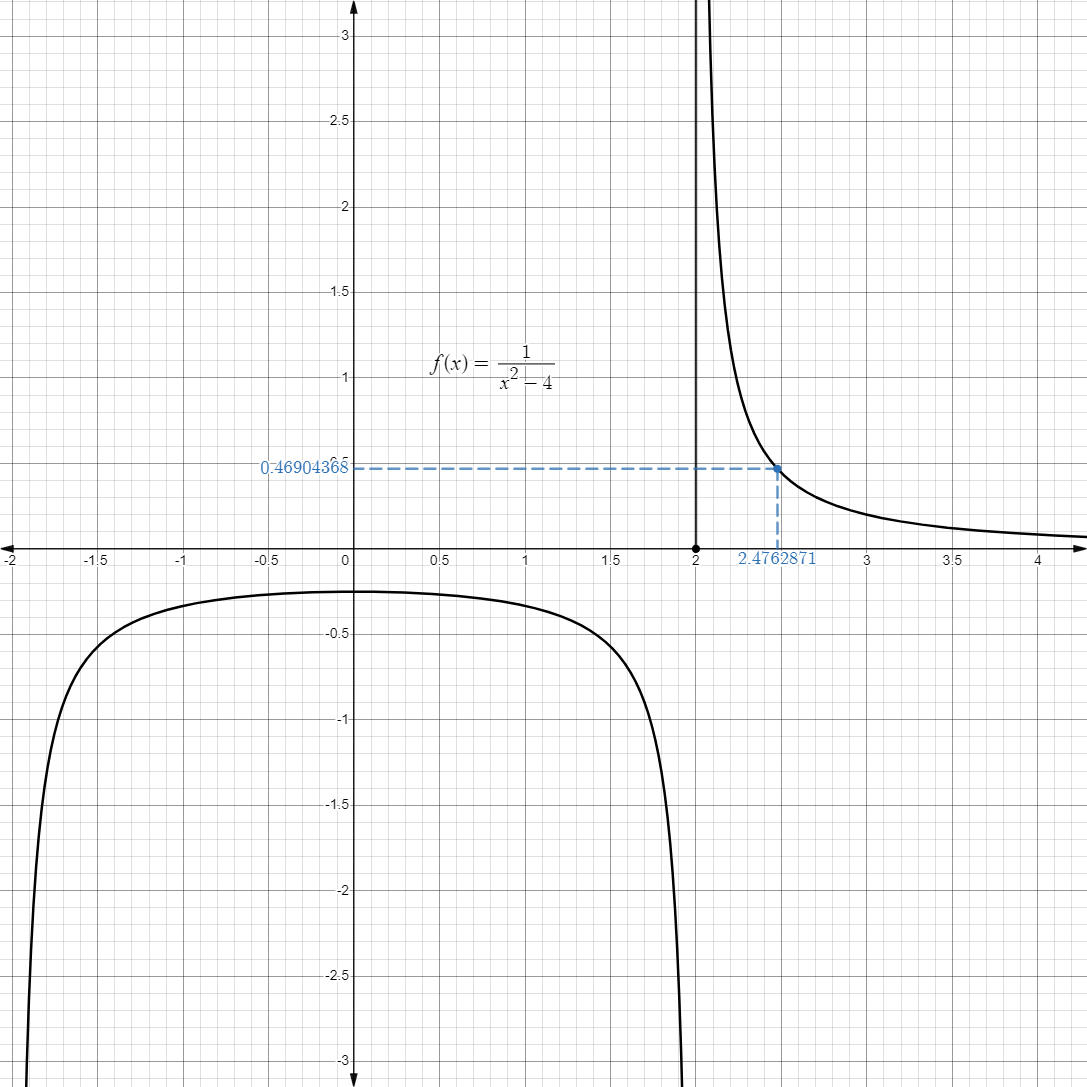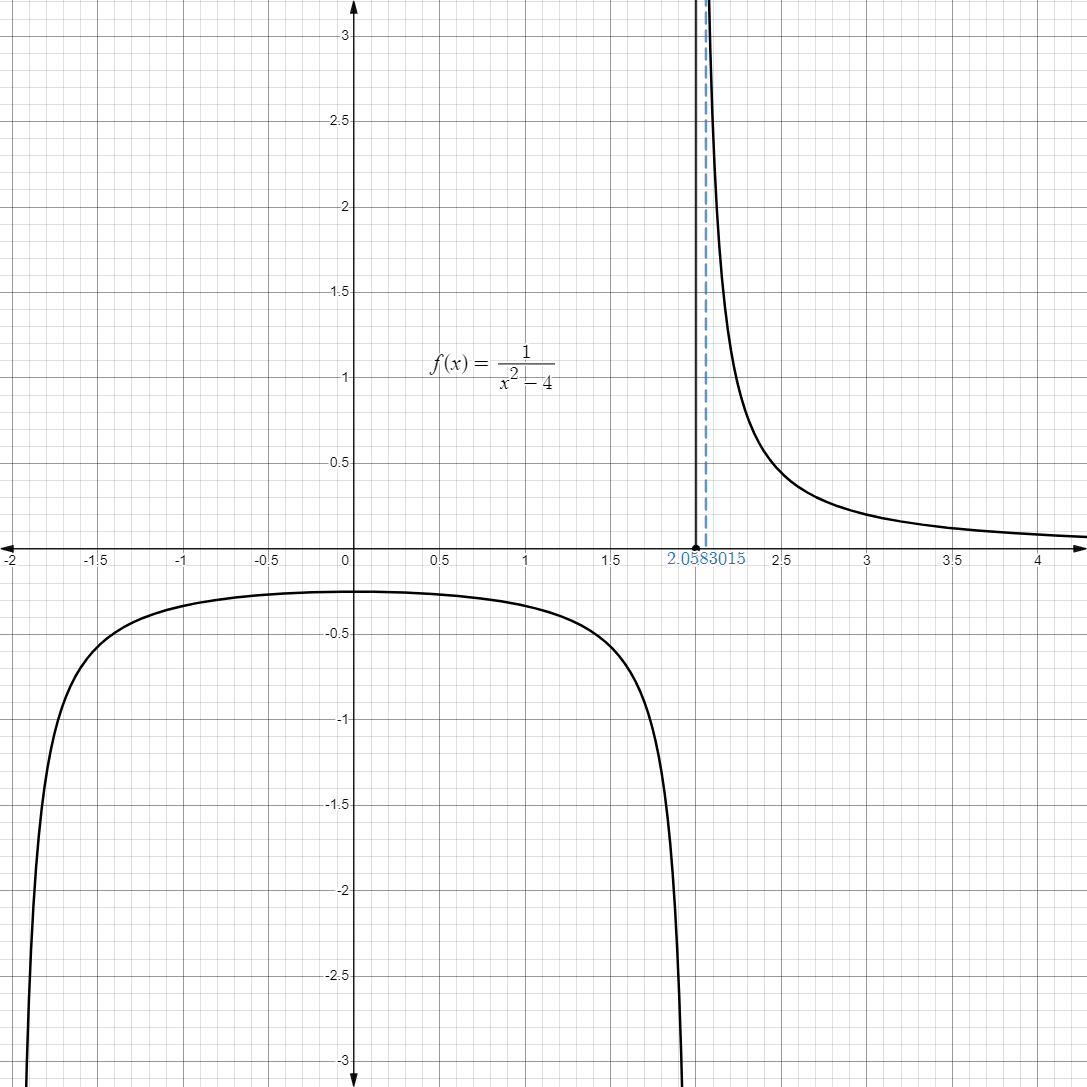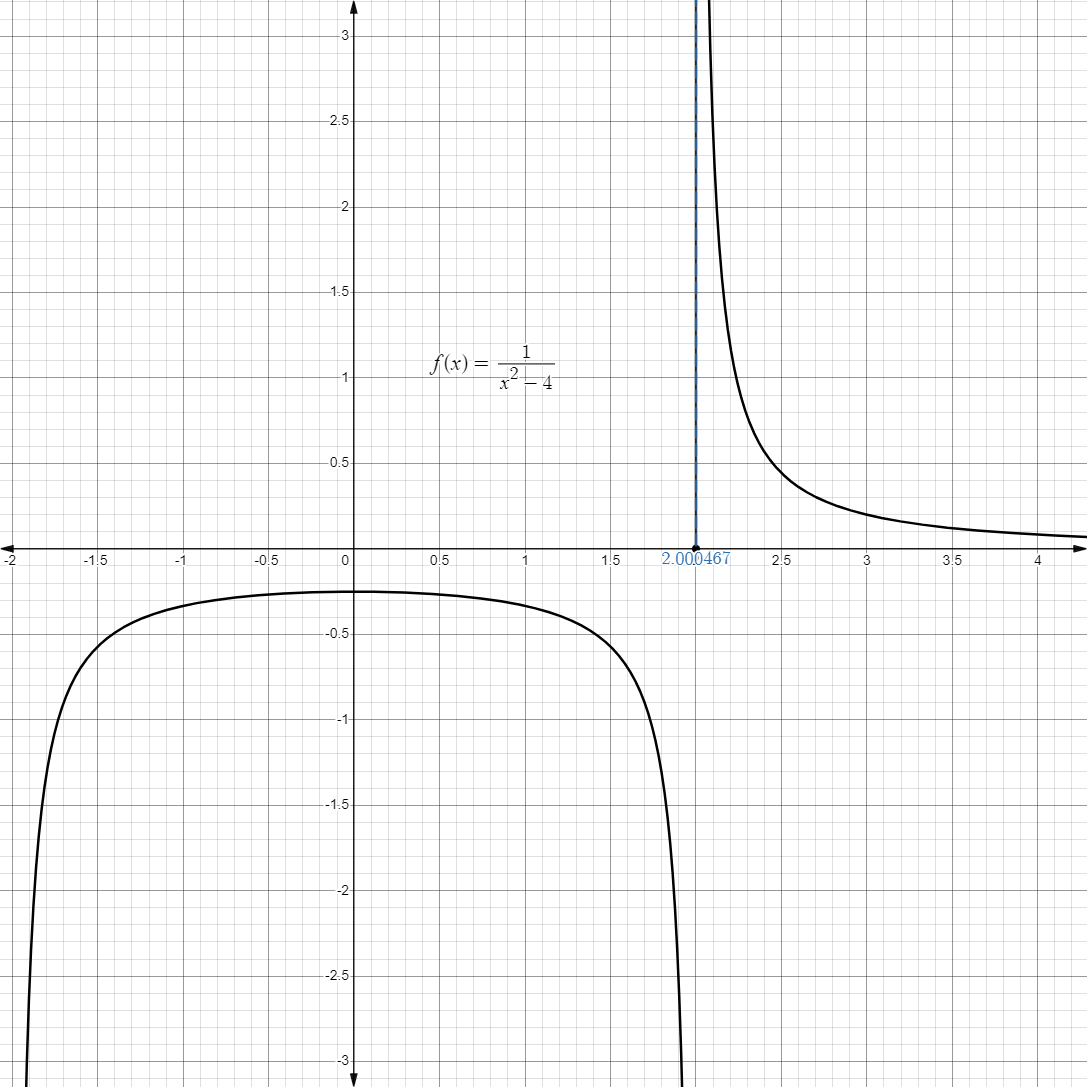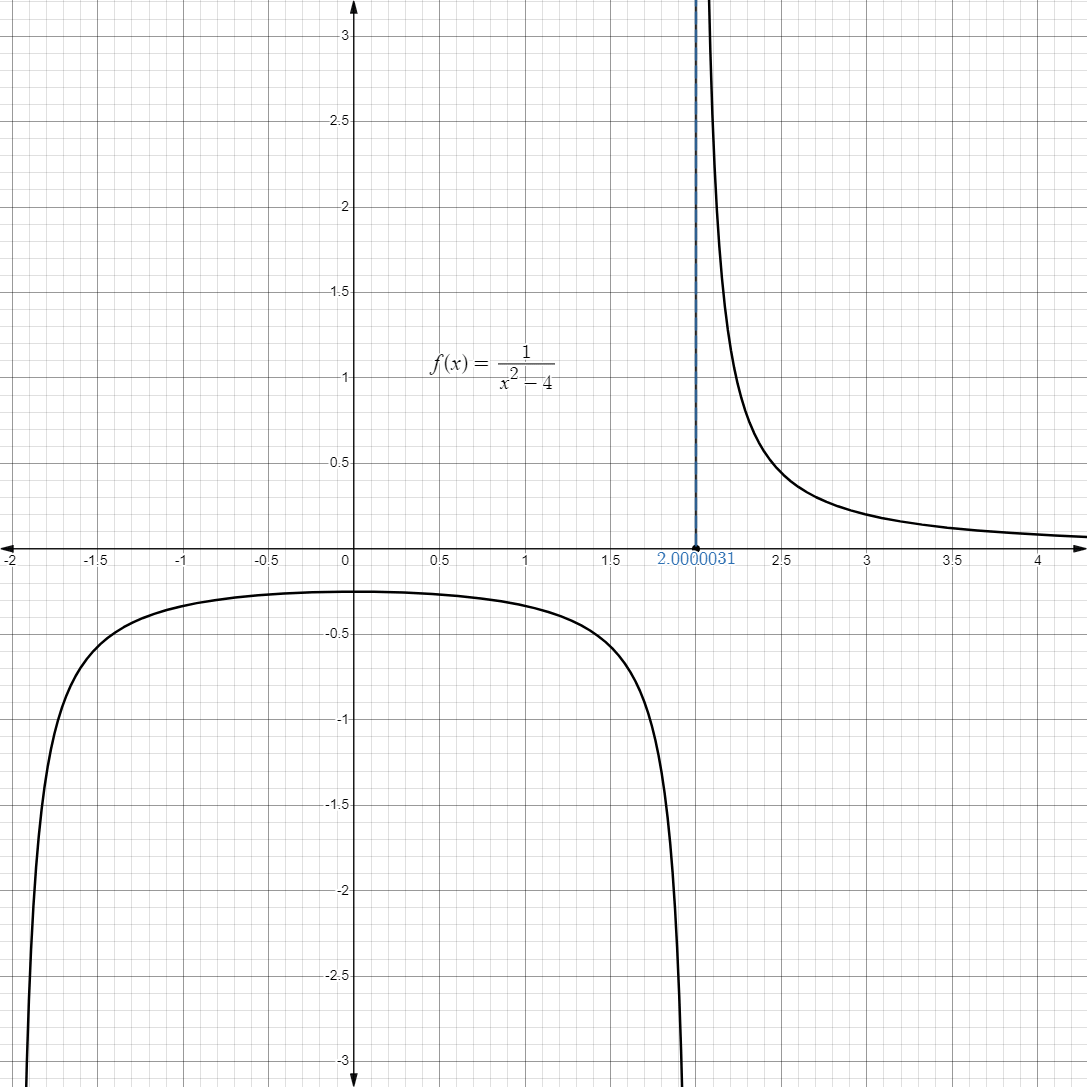
- Likewise, we can also approach
from the negative side starting from .
- Graphically, it may also look like this:
- No matter how close we get to
, it doesn’t seem to approach a single finite value as it just keeps getting larger and larger.
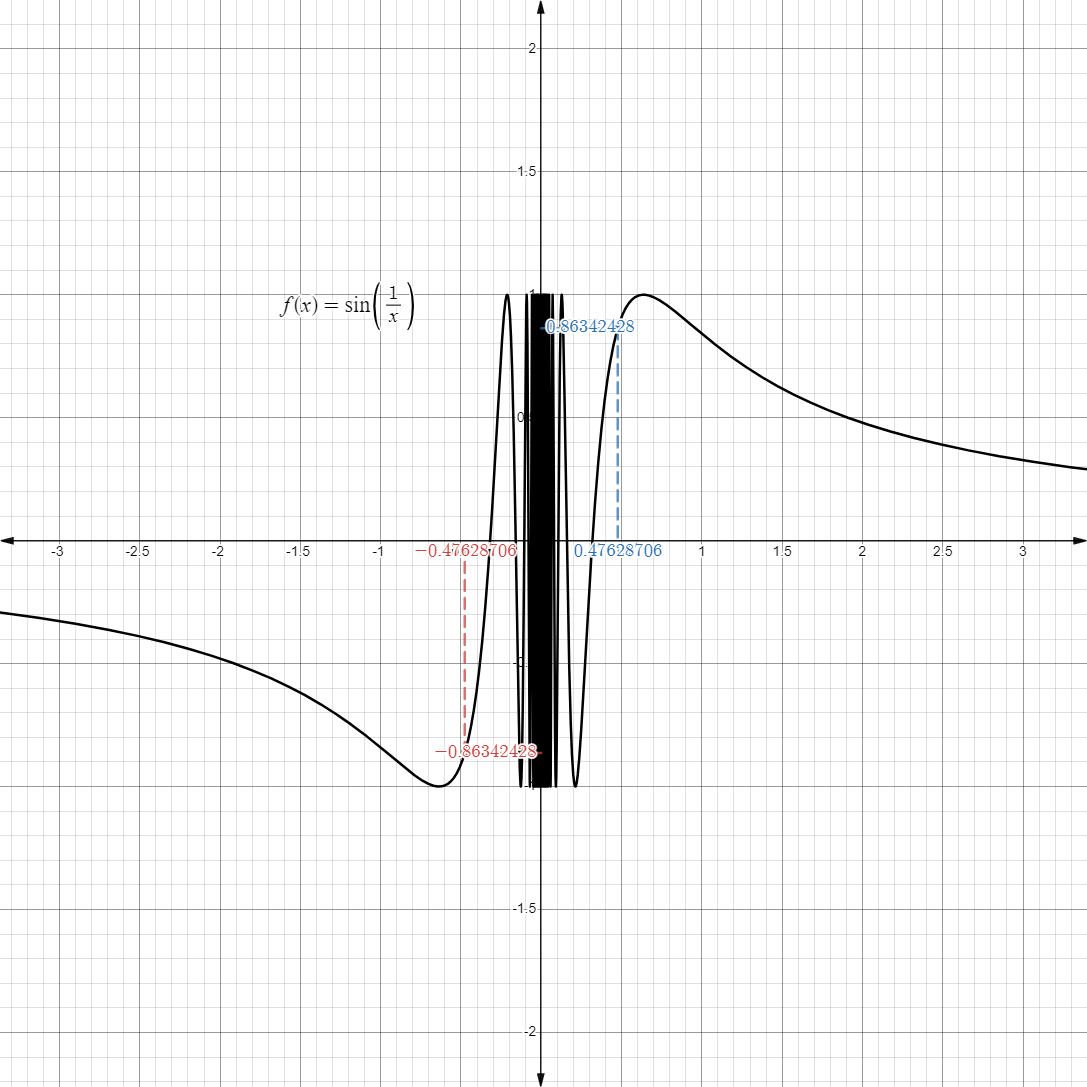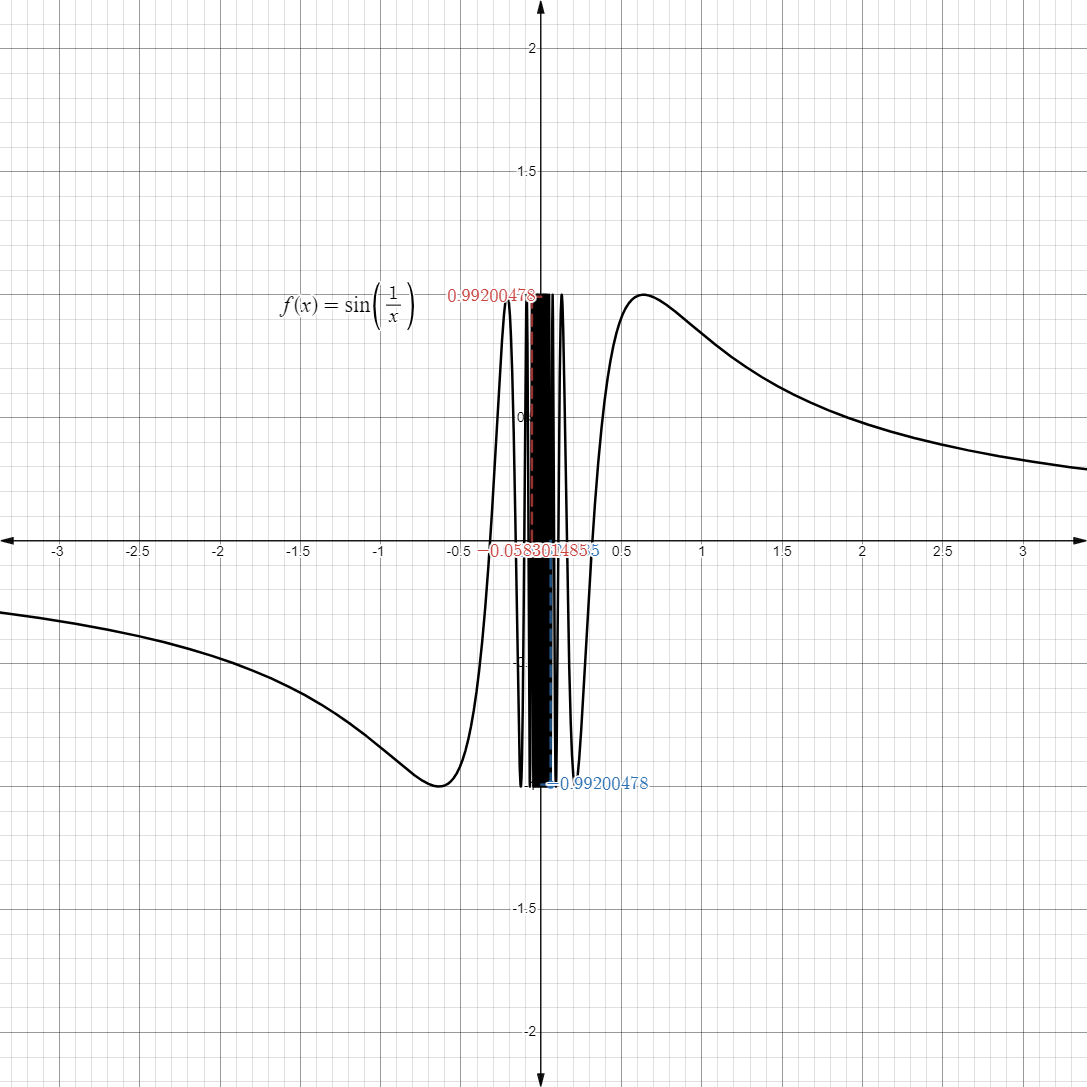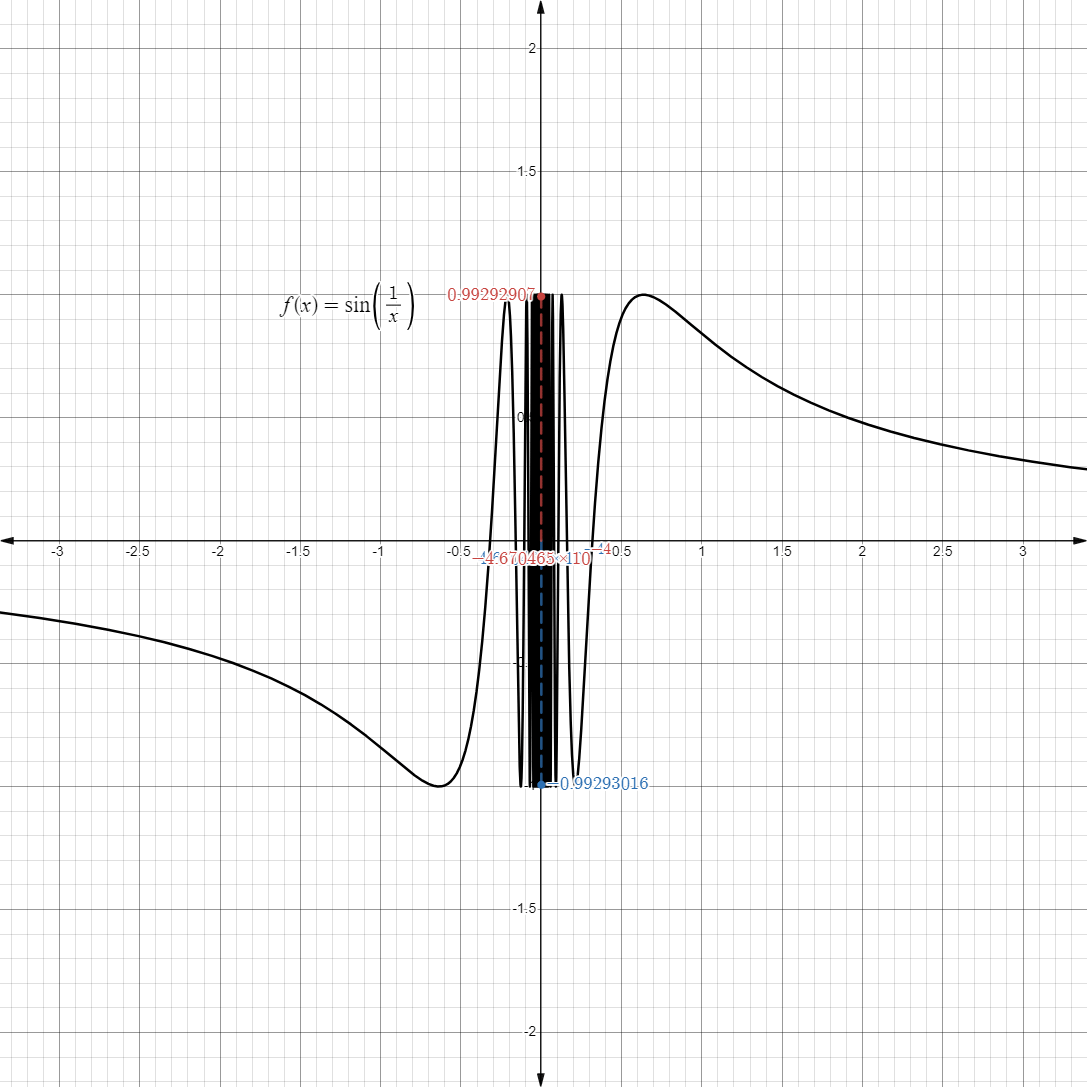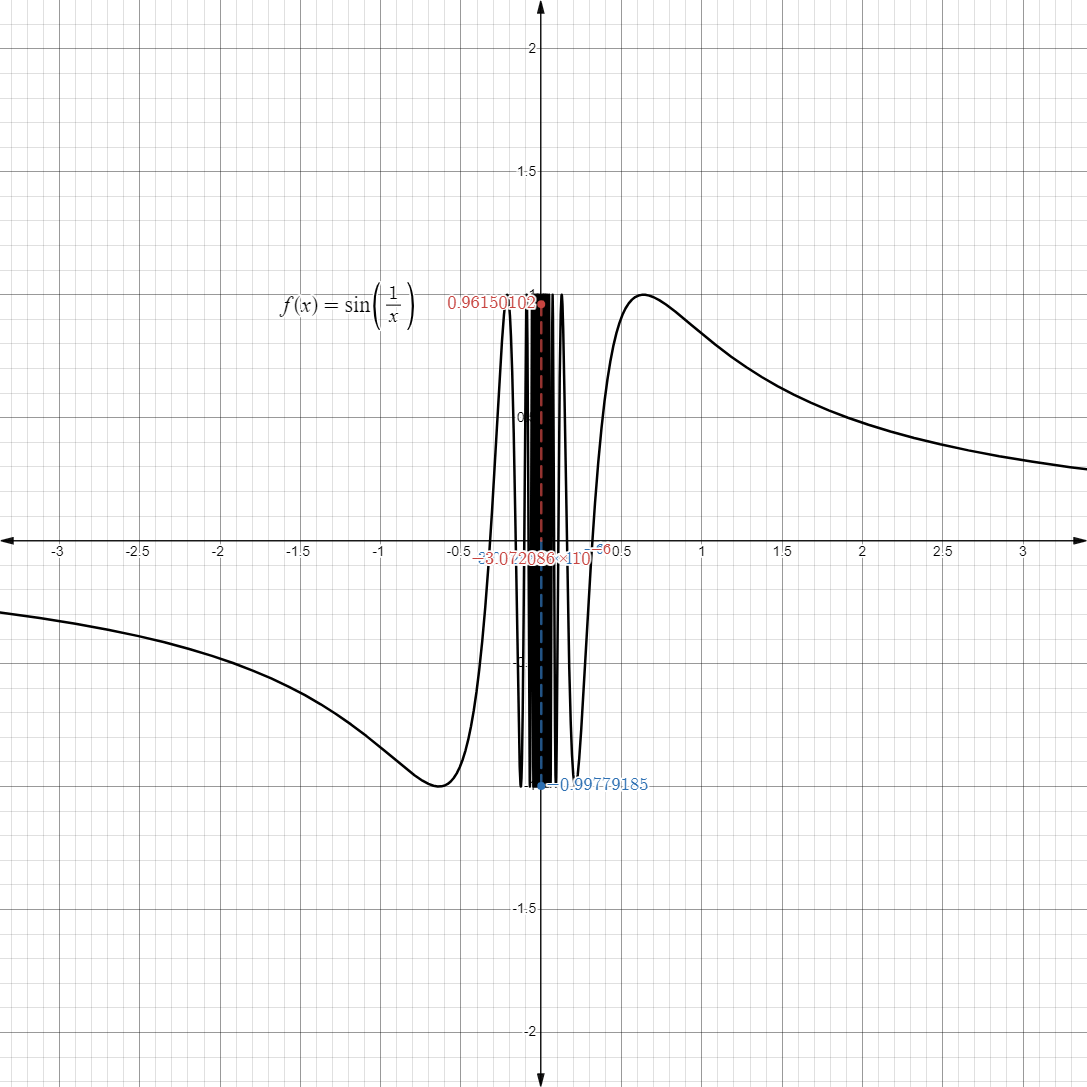
- Another unique limit is the one below:
- Taking a look at its graph, we see that as it approaches
, it oscillates really fast from to .
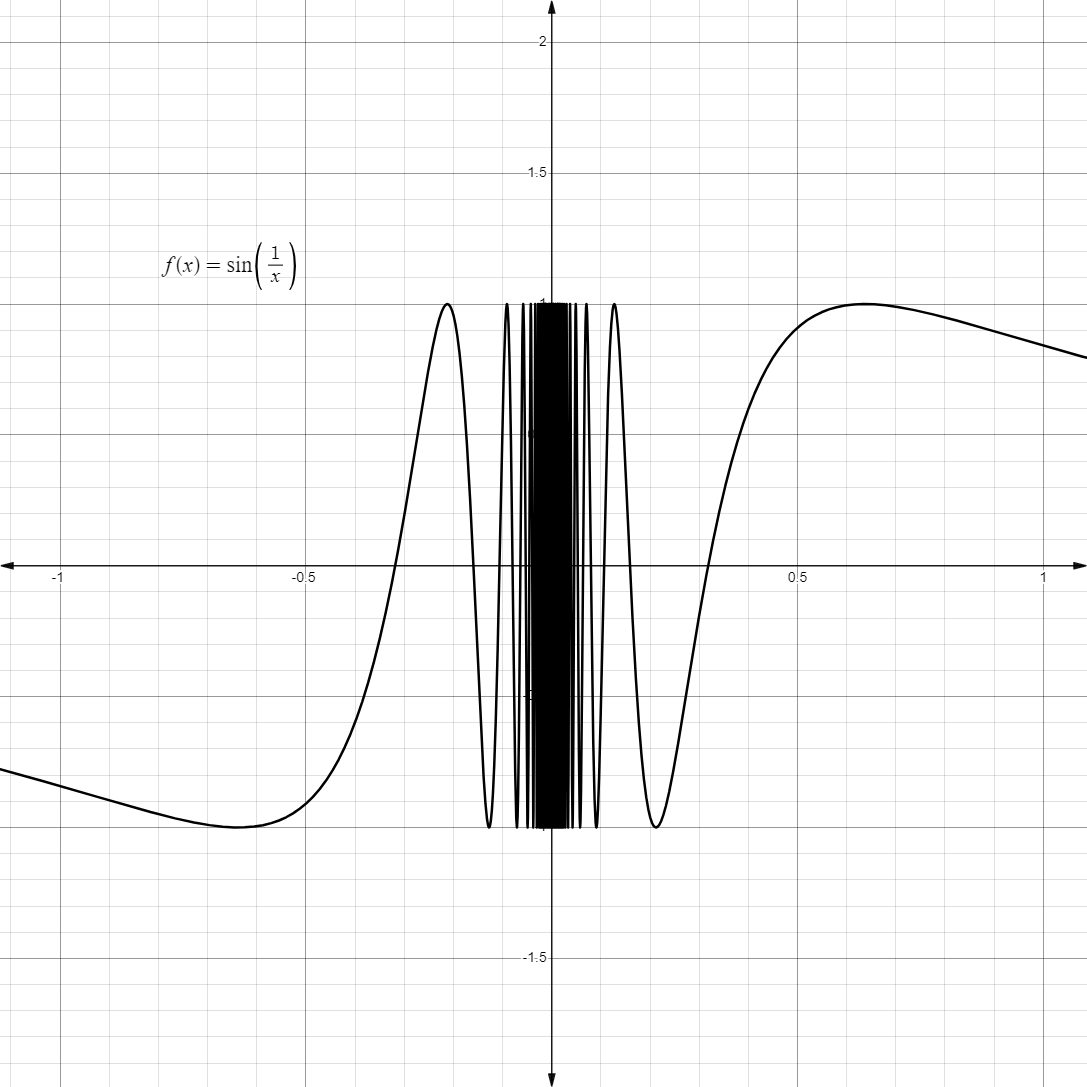
- We can also see that as it approaches
from either side, it doesn’t really approach on a fixed, finite value.
Definition
Existence of a Limit: Limit must be a Fixed, Finite ValueGiven a function
and a point , if:
goes unbounded or approaches or as , or doesn’t approach a single, fixed value, then
does not exist.